Question

【題目】如圖，某工廠與A、B兩地有公路、鐵路相連．這家工廠從A地購買一批每噸2000元的原料運回工廠，制成每噸7500元的產品運到B地．已知公路運價為2元/ (噸·千米)，鐵路運價為 1.5元/(噸·千米)，且這兩次運輸共支出公路運輸費2.6萬元，鐵路運輸費15.6萬元。

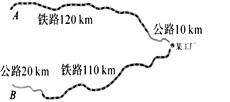
求：(1)該工廠從A地購買了多少噸原料？ 制成運往B地的產品多少噸？

(2)若不計人力成本，這批產品盈利多少元？ （盈利=銷售款-原料費-運輸費）

Answer 1

【答案】(1) 工廠從A地購買了500噸原料，制成運往B地的產品400噸; (2)不計人力成本，這批產品盈利1818000元．

【解析】試題分析：（1）設工廠從A地購買了x噸原料，制成運往B地的產品y噸，依據公路總運費等于2.6萬，鐵路總運費等于15.6萬列出關于x與y的二元一次方程組，求出方程組的解得到x與y的值即可；

（2）根據盈利＝銷售款－原料費－運輸費，即可求出所求的結果；

試題解析：

（1）設工廠從A地購買了x噸原料，制成運往B地的產品y噸．

依題意

整理得

解得

答：工廠從A地購買了500噸原料，制成運往B地的產品400噸．

（2）依題意得400×75000－500×2000－26000－156000

＝1818000(元)，

答：不計人力成本，這批產品盈利1818000元．