
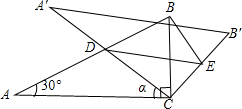
 交CB′于點E,連接BE.易知,在旋轉過程中,△BDE為直角三角形.設BC=1,AD=x,△BDE的面積為S.
交CB′于點E,連接BE.易知,在旋轉過程中,△BDE為直角三角形.設BC=1,AD=x,△BDE的面積為S.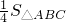 時,判斷⊙E與A′C的位置關系,并求相應的tanα值.
時,判斷⊙E與A′C的位置關系,并求相應的tanα值.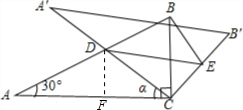 解:(1)∵∠A=a=30°,
解:(1)∵∠A=a=30°, BC=
BC= ,AB=2BC=2.
,AB=2BC=2. =
= ,
, x.
x. ×
× x(2-x)=-
x(2-x)=- x2+
x2+ x.(0<x<2)
x.(0<x<2) s△ABC
s△ABC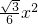 +
+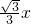 =
= ,
,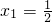 ,
,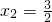 .
. 時,BD=2-
時,BD=2- =
= ,BE=
,BE= ×
× =
= .
. =
=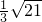 .
. DE=
DE=
 >BE,
>BE, 過D作DF⊥AC于F,則
過D作DF⊥AC于F,則 ,
,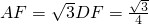 .
. .
.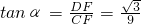 .
.  時,
時, ,
,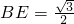 .
.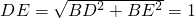 ,
, ,
, .
. ,由旋轉性質求得△ADC∽△BCE,根據比例關系式,求出S與x的函數關系式;
,由旋轉性質求得△ADC∽△BCE,根據比例關系式,求出S與x的函數關系式;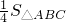 時,求得x的值,判斷⊙E和DE的長度大小,確定⊙E與A′C的位置關系,再求tanα值.
時,求得x的值,判斷⊙E和DE的長度大小,確定⊙E與A′C的位置關系,再求tanα值.

科目:初中數學 來源: 題型:
 C,△ABC的面積為S△ABC.
C,△ABC的面積為S△ABC.| 1 | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•蘄春縣模擬)如圖,將含30°角的直角三角尺ABC繞點B順時針旋轉150°后得到△EBD,連接CD.若AB=4cm.則△BCD的面積為( )
(2013•蘄春縣模擬)如圖,將含30°角的直角三角尺ABC繞點B順時針旋轉150°后得到△EBD,連接CD.若AB=4cm.則△BCD的面積為( )查看答案和解析>>
科目:初中數學 來源: 題型:
 交CB′于點E,連接BE.易知,在旋轉過程中,△BDE為直角三角形.設BC=1,AD=x,△BDE的面積為S.
交CB′于點E,連接BE.易知,在旋轉過程中,△BDE為直角三角形.設BC=1,AD=x,△BDE的面積為S.| 1 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com