
 的兩直角邊的長都是方程
的兩直角邊的長都是方程 的根,則Rt△
的根,則Rt△ 的斜邊長可能是 .(寫出所有可能的值)
的斜邊長可能是 .(寫出所有可能的值)科目:初中數(shù)學(xué) 來源:不詳 題型:解答題
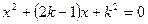 的兩根
的兩根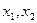 滿足
滿足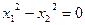 ,雙曲線
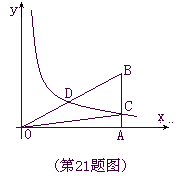
,雙曲線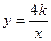 (x>0)經(jīng)過Rt△OAB斜邊OB的中點D,與直角邊AB交于C(如圖),求
(x>0)經(jīng)過Rt△OAB斜邊OB的中點D,與直角邊AB交于C(如圖),求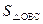 .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:單選題
 .若商店在試銷期間每天銷售這種商品獲得200元的利潤,根據(jù)題意,下面所列方程正確的是( ).
.若商店在試銷期間每天銷售這種商品獲得200元的利潤,根據(jù)題意,下面所列方程正確的是( ).A. | B. |
C. | D. |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:單選題
 +n2+2m-6n+10=0的是( )
+n2+2m-6n+10=0的是( )| A.m="1," n=3 | B.m=1,n=-3 | C.m=-1,n=-3 | D.m=-1,n=3 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com