
【題目】對一張矩形紙片ABCD進行折疊,具體操作如下:
第一步:先對折,使AD與BC重合,得到折痕MN,展開;
第二步:再一次折疊,使點A落在MN上的點A′處,并使折痕經過點B,得到折痕BE,同時,得到線段BA′,EA′,展開,如圖1;
第三步:再沿EA′所在的直線折疊,點B落在AD上的點B′處,得到折痕EF,同時得到線段B′F,展開,如圖2.
求證:(1)∠ABE=30°;
(2)四邊形BFB′E為菱形.
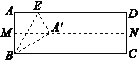

圖1 圖2
【答案】(1)30°;(2)見解析
【解析】
(1)由折疊的性質易得:∠ABE=∠A′BE,M是AB的中點,A′是EF的中點,∠EA′B=∠A=90°,由此可得BA′是EF的垂直平分線,從而可得BE=BF,由此可得∠A′BE=∠A′BF,從而可得∠ABE=∠A′BE=∠A′BF,這樣結合∠ABC=90°即可得到∠ABE=![]() ∠ABC=30°;
∠ABC=30°;
(2)由已知條件結合折疊的性質可得:BE=B′E,BF=B′F,這樣結合(1)中所得BE=BF即可得到四邊形BFB′E的四邊相等,由此即可得到四邊形BFB′E是菱形.
(1)∵對折使AD與BC重合,折痕是MN,
∴M是AB的中點,
∴A′是EF的中點.
∵∠BA′E=∠A=90°,
∴BA′垂直平分EF,
∴BE=BF,
∴∠A′BE=∠A′BF.
由翻折的性質,知∠ABE=∠A′BE,
∴∠ABE=∠A′BE=∠A′BF,
∴∠ABE=![]() ∠ABC=
∠ABC=![]() ×90°=30°;
×90°=30°;
(2)∵沿EA′所在的直線折疊,
點B落在AD上的點B′處,
∴BE=B′E,BF=B′F.
∵BE=BF,
∴BE=B′E=B′F=BF,
∴四邊形BFB′E為菱形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】由一些正整數組成的數表如下(表中下一行中數的個數是上一行中數的個數的2倍):

若規定坐標號(m,n)表示第m行從左向右第n個數,則(7,4)所表示的數是_____;(5,8)與(8,5)表示的兩數之積是_______;數2012對應的坐標號是_________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,直線AB:y=x+b交y軸于點A(0,4),交x軸于點B.
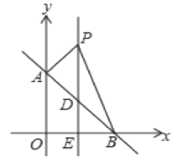
(1)求點B的坐標;
(2)直線l垂直平分OB交AB于點D,交x軸于點E,點P是直線l上一動點,且在點D的上方,設點P的縱坐標為n.
①用含n的代數式表示△ABP的面積;
②當S△ABP=8時,求點P的坐標;
(3)在(2)中②的條件下,以PB為斜邊作等腰直角△PBC,求點C的坐標。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC繞點A逆時針旋轉80°后得到△A′B′C′(點B的對應點是點B′,點C的對應點是點C′,連接BB′,若∠B′BC=20°,則∠BB′C′的大小是( )
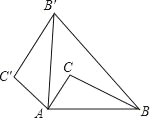
A. 82° B. 80° C. 78° D. 76°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某市有一塊長為(3a+b)米、寬為(2a+b)米的長方形地塊,中間是邊長為(a+b)米的正方形,規劃部門計劃將在中間的正方形修建一座雕像,四周的陰影部分進行綠化.
(1)綠化的面積是多少平方米?(用含字母a、b的式子表示)
(2)求出當a=10,b=12時的綠化面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 是中線,作
是中線,作![]() 關于
關于![]() 的軸對稱圖形
的軸對稱圖形![]() .
.
(1)直接寫出![]() 和
和![]() 的位置關系;
的位置關系;
(2)連接![]() ,寫出
,寫出![]() 和
和![]() 的數量關系,并說明理由;
的數量關系,并說明理由;
(3)當![]() ,
,![]() 時,在
時,在![]() 上找一點
上找一點![]() ,使得點
,使得點![]() 到點
到點![]() 與到點
與到點![]() 的距離之和最下小,求
的距離之和最下小,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明同學在完成第10章的學習后,遇到了一些問題,請你幫助他.
(1)圖1中,當![]() ,試說明
,試說明![]() .
.
(2)圖2中,若![]() ,則
,則![]() 嗎?請說明理由.
嗎?請說明理由.
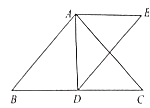
(3)圖3中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() ______(直接寫出結果,用含x,y,z的式子表示)
______(直接寫出結果,用含x,y,z的式子表示)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題
情景:

試根據圖中的信息,解答下列問題:
(1)購買6根跳繩需___________元,購買12根跳繩需_____________元.
(2)小紅比小明多買2根,付款時小紅反而比小明少5元,你認為有這種可能嗎?若有,請求出小紅購買跳繩的根數;若沒有,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com