
求拋物線y=x2-4x+3關于y軸對稱的拋物線的表達式.
(1)在同一直角坐標系中,畫出兩拋物線;
(2)根據所畫圖像,說明兩拋物線的關系.
|
[答案]∵- ∴拋物線y=x2-4x+3的頂點坐標為(2,-1). 由已知得,所求拋物線的開口方向和形狀與原拋物線相同,其頂點與原拋物線的頂點關于 y軸對稱.故所求拋物線的表達式為 y=(x+2)2-1,即y=x2+4x+3.(1)它們的圖像如圖所示.
(2)兩拋物線開口方向相同,形狀相同,只是位置不同,它們屬于平移關系.即拋物線y=x2+4x+3也可看成拋物線y=x2-4x+3向左平移4個單位所得. [剖析]在對拋物線進行對稱、平移等變換時,拋物線的形狀不變,其頂點也被進行了相應變換.因此,在求變換后的表達式時,關鍵是確定其開口方向和頂點坐標. |
|
[方法提煉] 求拋物線關于 x軸、y軸、原點的對稱圖形的表達式時,先求出原拋物線的頂點坐標及對稱拋物線的開口方向,再確定對稱拋物線的頂點坐標,并寫出其表達式. |


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:初中數學 來源:學習周報 數學 滬科九年級版 2009-2010學年 第2期 總第158期 滬科版 題型:044
已知關于
x的一元二次方程x2+mx+n=0的兩根是x1=-3,x2=4,求拋物線y=x2+mx+n的頂點坐標和對稱軸.查看答案和解析>>
科目:初中數學 來源:新課程 新理念 新思維·同步練習篇·數學 九年級下冊(蘇教版) 蘇教版 題型:044
先閱讀下面一段材料,再完成后面的問題:
材料 過拋物線y=ax2(a>0)的對稱軸上一點(0,-![]() ),作對稱軸的垂線l,則拋物線上任意一點P到點F(0,
),作對稱軸的垂線l,則拋物線上任意一點P到點F(0,![]() )的距離與P到l的距離一定相等,我們將點F與直線l分別稱作這拋物線的焦點和準線,如y=x2的焦點為(0,
)的距離與P到l的距離一定相等,我們將點F與直線l分別稱作這拋物線的焦點和準線,如y=x2的焦點為(0,![]() ).
).
問題 若直線y=kx+b交拋物線y=![]() x2于A、B兩點,AC、BD垂直于拋物線的準線l,垂直足分別為C、D(如圖).
x2于A、B兩點,AC、BD垂直于拋物線的準線l,垂直足分別為C、D(如圖).
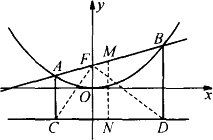
(1)求拋物線y=![]() x2的焦點F的坐標;
x2的焦點F的坐標;
(2)求證:直線AB過焦點時,CF⊥DF;
(3)當直線AB過點(-1,0),且以線段AB為直徑的圓與準線l相切時,求這條直線對應的函數解析式.
查看答案和解析>>
科目:初中數學 來源:2011屆河南省扶溝縣初三下冊26章《用函數觀點看一元二次方程》檢測題 題型:解答題
拋物線y=x2+x-k與直線y=-2x+1的交點的縱坐標為3。
(1)求拋物線的解析式
(2)求拋物線y=x2+x-k與直線y=-2x+1的另一個交點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com