【問題引入】
幾個人拎著水桶在一個水龍頭前面排隊打水,水桶有大有小.他們該怎樣排隊才能使得總的排隊時間最短?
假設只有兩個人時,設大桶接滿水需要T分鐘,小桶接滿水需要t分鐘(顯然T>t),若拎著大桶者在拎著小桶者之前,則拎大桶者可直接接水,只需等候T分鐘,拎小桶者一共等候了(T+t)分鐘,兩人一共等候了(2T+t)分鐘;反之,若拎小桶者在拎大桶者前面,容易求出出兩人接滿水等候(T+2t)分鐘.可見,要使總的排隊時間最短,拎小桶者應排在拎大桶者前面.這樣,我們可以猜測,幾個人拎著水桶在一個水龍頭前面排隊打水,要使總的排隊時間最短,需將他們按水桶從小到大排隊.
規律總結:
事實上,只要不按從小到大的順序排隊,就至少有緊挨著的兩個人拎著大桶者排在拎小桶者之前,仍設大桶接滿水需要T分鐘,小桶接滿水需要t分鐘,并設拎大桶者開始接水時已等候了m分鐘,這樣拎大桶者接滿水一共等候了(m+T)分鐘,拎小桶者一共等候了(m+T+t)分鐘,兩人一共等候了(2m+2T+t)分鐘,在其他人位置不變的前提下,讓這兩個人交還位置,即局部調整這兩個人的位置,同樣介意計算兩個人接滿水共等候了______分鐘,共節省了______分鐘,而其他人等候的時間未變,這說明只要存在有緊挨著的兩個人是拎大桶者在拎小桶者之前都可以這樣調整,從而使得總等候時間減少.這樣經過一系列調整后,整個隊伍都是從小打到排列,就打到最優狀態,總的排隊時間就最短.
【方法探究】
一般的,對某些設計多個可變對象的數學問題,先對其少數對象進行調整,其他對象暫時保持不變,從而化難為易,取得問題的局部解決.經過若干次這種局部的調整,不斷縮小范圍,逐步逼近目標,最終使問題得到解決,這種數學思想就叫做局部調整法.
【實踐應用1】
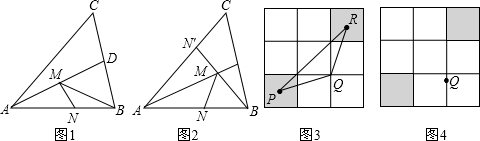
如圖1在銳角△ABC中,AB=

,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是多少?
解析:
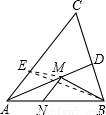
(1)先假定N為定點,調整M到合適的位置使BM+MN有最小值(相對的),容易想到,在AC上作AN′=AN(即作點N關于AD的對稱點N'),連接BN′交AD于M,則M點是使BM+MN有相對最小值的點.(如圖2,M點是確定方法找到的)
(2)在考慮點N的位置,使BM+MN最終達到最小值.可以理解,BM+MN=BM+MN′,所以要使BM+MN′有最小值,只需使______,此時BM+MN的最小值是______.
【實踐應用2】
如圖3,把邊長是3的正方形等分成9個小正方形,在有陰影的小正方形內(包括邊界)分別取點P、R,于已知格點Q(每個小正方形的頂點叫做格點)構成三角形,則△PQR的最大面積是______,請在圖4中畫出面積最大時的△PQR的圖形.


 ,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分線交BC于點D,M、N分別是AD和AB上的動點,則BM+MN的最小值是多少?
 解:如圖,在AC上截取AE=AN,連接BE.
解:如圖,在AC上截取AE=AN,連接BE.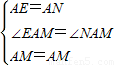 ,
, ,∠BAC=45°,此時,△ABE為等腰直角三角形,
,∠BAC=45°,此時,△ABE為等腰直角三角形,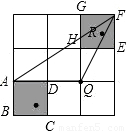 當P在A的位置時,R在線段GF上時,△PQR的面積最大,最大面積是:
當P在A的位置時,R在線段GF上時,△PQR的面積最大,最大面積是: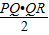 =
=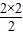 =2.
=2.

 名校課堂系列答案
名校課堂系列答案