(1)證明:∵點O、O′關于直線y=x+b的對稱,
∴直線y=x+b是線段OO′的垂直平分線,∴AO=AO′,BO=BO′。
又∵OA,OB是⊙O的半徑,∴OA=OB。
∴AO=AO′=BO=BO′。∴四邊形OAO′B是菱形.
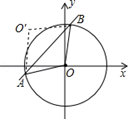
(2)解:如圖,設直線y=x+b與x軸、y軸的交點坐標分別是

N(-b,0),P(0,b),AB與OO′相交于點M。
則△ONP為等腰直角三角形,∴∠OPN=45°。
∵四邊形OAO′B是菱形,∴OM⊥PN。
∴△OMP為等腰直角三角形。
當點O′落在圓上時,OM=
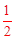
OO′=1。
在Rt△OMP中,由勾股定理得:OP=
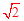
,即b=
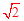
。


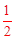 OO′=1。
OO′=1。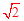 ,即b=
,即b=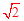 。
。
