【答案】
分析:(1)過D作DM∥PE交CP的延長線于M,根據平行線分線段成比例定理求出PM=PD,推出∠M=∠PDM,根據平行線的性質得出∠M=∠CPE,∠DPE=∠PDM,即可得出答案;
(2)根據切割線定理得出AQ
2=AP×AB,證△APC∽△DPB,推出
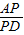
=
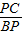
,得出AP×BP=PC×PD,代入即可得出答案.
解答:(1)證明:
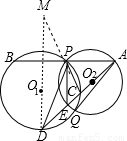
過D作DM∥PE交CP的延長線于M,
則

=
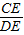
,
∵
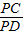
=
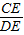
,
∴PM=PD,
∴∠M=∠PDM,
∵PE∥MD,
∴∠M=∠CPE,∠DPE=∠PDM,
∴∠CPE=∠DPE;
(2)
證明:連接BD,
∵O
2在AE上,
∴∠APE=∠BPE=90°,
∵∠CPE=∠DPE,
∴∠APC=∠BPD,
∵P、B、D、C四點共圓,
∴∠ACP=∠B,
∴△APC∽△DPB,
∴
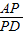
=

,
∴AP×BP=PC×PD,
∵AQ切⊙O
1于Q,APB是⊙O
1的割線,
∴AQ
2=AP×AB,
∴AQ
2-AP
2=AP×AB-AP
2=AP(AB-AP)=AP×BP=PC•PD,
即AQ
2-AP
2=PC•PD.
點評:本題考查了相似三角形的性質和判定,圓內接四邊形的性質,等腰三角形的性質,平行線分線段成比例定理等知識點的應用,主要考查學生綜合運用性質進行推理的能力.

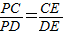 ,過A作⊙O1的切線AQ,切點為Q.求證:
,過A作⊙O1的切線AQ,切點為Q.求證: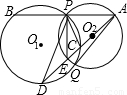
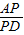 =
=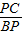 ,得出AP×BP=PC×PD,代入即可得出答案.
,得出AP×BP=PC×PD,代入即可得出答案. 過D作DM∥PE交CP的延長線于M,
過D作DM∥PE交CP的延長線于M, =
=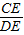 ,
,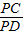 =
=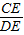 ,
, 證明:連接BD,
證明:連接BD,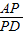 =
= ,
,

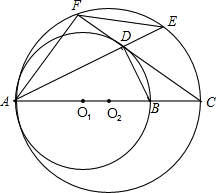 O1于點D,AD的延長線交⊙O2于點E,連接AF、EF、BD.
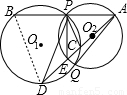
O1于點D,AD的延長線交⊙O2于點E,連接AF、EF、BD.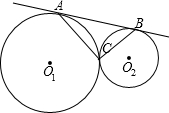 已知:如圖,⊙O1與⊙O2外切于C點,AB一條外公切線,A、B分別為切點,連接AC、BC.設⊙O1的半徑為R,⊙O2的半徑為r,若tan∠ABC=
已知:如圖,⊙O1與⊙O2外切于C點,AB一條外公切線,A、B分別為切點,連接AC、BC.設⊙O1的半徑為R,⊙O2的半徑為r,若tan∠ABC=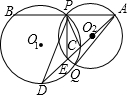 (1998•南京)已知,如圖,⊙O1與⊙O2相交,點P是其中一個交點,點A在⊙O2上,AP的延長線交⊙O1于點B,AO2的延長線交⊙O1于點C、D,交⊙O2于點E,連接PC、PE、PD,且
(1998•南京)已知,如圖,⊙O1與⊙O2相交,點P是其中一個交點,點A在⊙O2上,AP的延長線交⊙O1于點B,AO2的延長線交⊙O1于點C、D,交⊙O2于點E,連接PC、PE、PD,且