
| 1 |
| 2 |
| 1 |
| 2 |
 解:(1)作GM⊥HE,
解:(1)作GM⊥HE,| 1 |
| 2 |
| 1 |
| 2 |
| a-b |
| 2 |
| a-b |
| 2 |
| m-2n |
| 4 |
| m-2n |
| 4 |


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:初中數學 來源:2011年北京市朝陽區(qū)九年級綜合練習(二)數學卷 題型:解答題
閱讀材料并解答問題
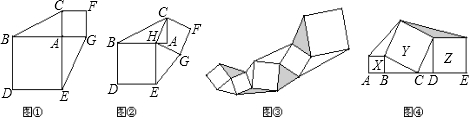
如圖①,以Rt△ABC的直角邊AB、AC為邊分別向外作正方形ABDE和正方形ACFG,連結EG,可以得出結論△ABC的面積與△AEG的面積相等.
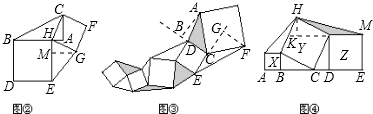
(1)在圖①中的△ABC的直角邊AB上任取一點H,連結CH,以BH、HC為邊分別向外作正方形HBDE和正方形HCFG,連結EG,得到圖②,則△HBC的面積與△HEG的面積的大小關系為 .
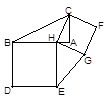
(2)如圖③,若圖形總面積是a,其中五個正方形的面積和是b,則圖中陰影部分的面積是 .
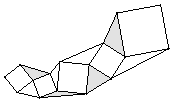
(3)如圖④,點A、B、C、D、E都在同一直線上,四邊形X、Y、Z都是正方形,若圖形總面積是m,正方形Y的面積是n,則圖中陰影部分的面積是 .
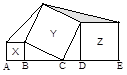
圖① 圖② 圖③ 圖④
查看答案和解析>>
科目:初中數學 來源:2011年北京市朝陽區(qū)九年級綜合練習(二)數學卷 題型:解答題
閱讀材料并解答問題
如圖①,以Rt△ABC的直角邊AB、AC為邊分別向外作正方形ABDE和正方形ACFG,連結EG,可以得出結論△ABC的面積與△AEG的面積相等.
(1)在圖①中的△ABC的直角邊AB上任取一點H,連結CH,以BH、HC為邊分別向外作正方形HBDE和正方形HCFG,連結EG,得到圖②,則△HBC的面積與△HEG的面積的大小關系為 .
(2)如圖③,若圖形總面積是a,其中五個正方形的面積和是b,則圖中陰影部分的面積是 .
(3)如圖④,點A、B、C、D、E都在同一直線上,四邊形X、Y、Z都是正方形,若圖形總面積是m,正方形Y的面積是n,則圖中陰影部分的面積是 .

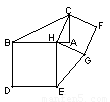


圖① 圖② 圖③ 圖④
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2011年北京市朝陽區(qū)中考數學二模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com