已知直線y=2x+6與x軸、y軸的交點分別為A、B,又P、Q兩點的坐標分別為P(-2,0)、Q(0,k),其中k<6.再以Q點為圓心,PQ長為半徑作圓,則:
(1)當k取何值時,⊙Q與直線相切?
(2)說出k在什么范圍內取值時,⊙Q與直線AB相離?相交?(只須寫出結果,不必寫解答過程)
【答案】
分析:(1)求出A、B的坐標,過Q所作QD⊥AB垂足為D,證Rt△QDB∽Rt△AOB,求出QD,根據QD=PQ,即可求出k的值;
(2)根據(1)的結論和⊙Q與直線AB相離、相交的特點即可求出答案.
解答:解:(1)把x=0代入y=2x+6得:y=6,
把y=0代入y=2x+6得:x=-3,
∴A(-3,O),B(0,6),
如圖,過Q所作QD⊥AB垂足為D
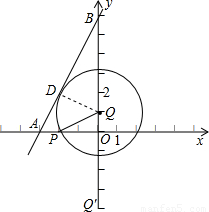
由勾股定理得:AB=3
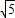
,
∵∠ABO=∠ABO,∠AOB=∠QDB=90°,
∴Rt△QDB∽Rt△AOB,AO=3,QB=6-k,AB=3
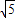
,
∴QD=
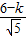
.
又QP=

,
∴

=
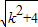
,
解得:k=-4或k=1,
故當k=-4或k=1時,⊙Q與直線AB相切;
(2)當-4<k<1時,⊙Q與直線AB相離;
當k<-4或1<k<6時,⊙Q與直線AB相交.
點評:本題考查了相似三角形的性質和判定,直線與圓的位置關系的應用,關鍵是求出k為何值時直線與圓相切,注意:當直線與圓相切時,d=r,當直線與圓相離時,d>r,當直線與圓相交時,d<r.

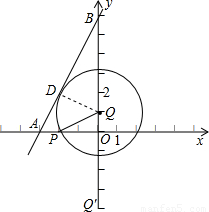
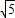 ,
,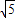 ,
,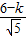 .
. ,
, =
=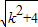 ,
,

 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案