
【題目】某班數學興趣小組對函數![]() 的圖象和性質進行了探究,探究過程如下,請補充完整:
的圖象和性質進行了探究,探究過程如下,請補充完整:
(1)自變量![]() 的取值范圍是全體實數,
的取值范圍是全體實數, ![]() 與
與![]() 的幾組對應值如下:
的幾組對應值如下:
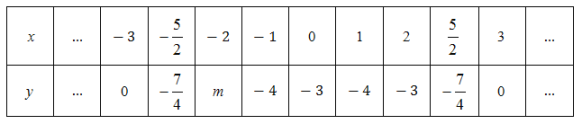
其中,![]() ________.
________.
(2)根據表中數據,在如圖所示的平面直角坐標系中描點,并畫出了函數圖象的一部分,請畫出該函數圖象的另一部分.
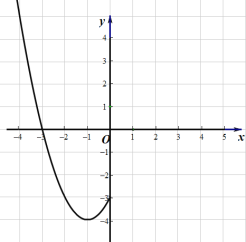
(3)觀察函數![]() 圖象,回答下列問題:
圖象,回答下列問題:
①函數圖像的對稱性是: .
②當![]() 時,寫出
時,寫出![]() 隨
隨![]() 的變化規律: .
的變化規律: .
(4)進一步探究函數圖象發現:方程![]() 有________個實數根.
有________個實數根.
【答案】(1)-3;(2)見解析;(3)①關于![]() 軸對稱;②當
軸對稱;②當![]() 時
時![]() 隨
隨![]() 的增大而減小,當
的增大而減小,當![]() 時
時![]() 隨
隨![]() 的增大而增大;(4)3.
的增大而增大;(4)3.
【解析】
(1)根據已知,將![]() 及其對應的自變量
及其對應的自變量![]() 代入函數解析式,即可求得
代入函數解析式,即可求得![]() 的值;
的值;
(2)根據表格中的數據,進行描點即可畫出函數圖象;
(3)觀察函數圖象即可得出對稱性和![]() 時,
時,![]() 隨
隨![]() 的變化規律,分為
的變化規律,分為![]() 時和
時和![]() 時兩種情況;
時兩種情況;
(4)直接觀察圖象即可得解.
(1)由已知,將![]() 及其對應的自變量
及其對應的自變量![]() 代入函數解析式,得
代入函數解析式,得
![]()
![]()
(2)如圖所示:

(3)觀察函數![]() 圖象,回答下列問題:
圖象,回答下列問題:
①函數圖像的對稱性是: 關于![]() 軸對稱
軸對稱
②當x > 0時,寫出y隨x的變化規律: 當![]() 時
時![]() 隨
隨![]() 時
時![]() 隨
隨![]() 的增大而增大 ;
的增大而增大 ;
(4)進一步探究函數圖象發現:方程![]() 有__
有__![]() __個實數根.
__個實數根.


 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ACB中,∠C=90°,AC=3,BC=4,O是BC的中點,到點O的距離等于![]() BC的所有點組成的圖形記為G,圖形G與AB交于點D.
BC的所有點組成的圖形記為G,圖形G與AB交于點D.

(1)補全圖形并求線段AD的長;
(2)點E是線段AC上的一點,當點E在什么位置時,直線ED與 圖形G有且只有一個交點?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC的頂點都在方格線的交點(格點)上.
(1)將△ABC繞C點按逆時針方向旋轉90°得到△A′B′C′,請在圖中畫出△A′B′C′.
(2)將△ABC向上平移1個單位,再向右平移5個單位得到△A″B″C″,請在圖中畫出△A″B″C″.
(3)若將△ABC繞原點O旋轉180°,A的對應點A1的坐標是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
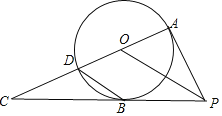
【題目】如圖,PA是⊙O的切線,A為切點.B為⊙O上一點,連接AO并延長,交⊙O于點D.交PB的延長線于點C連接PO,若PA=PB.
(1)求證:PB是⊙O的切線;
(2)連接DB,若∠C=30°,求證:D是CO的中點.
查看答案和解析>>
科目:初中數學 來源: 題型:
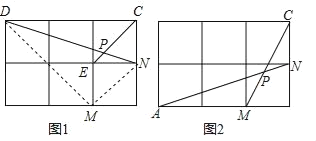
【題目】(問題呈現)如圖1,在邊長為1的正方形網格中,連接格點D,N和E,C,DN和EC相交于點P,求tan∠CPN的值.
(方法歸納)求一個銳角的三角函數值,我們往往需要找出(或構造出)一個直角三角形.觀察發現問題中∠CPN不在直角三角形中,我們常常利用網格畫平行線等方法解決此類問題,比如連接格點M,N,可得MN∥EC,則∠DNM=∠CPN,連接DM,那么∠CPN就變換到Rt△DMN中.
(問題解決)(1)直接寫出圖1中tan∠CPN的值為 ;
(2)如圖2,在邊長為1的正方形網格中,AN與CM相交于點P,求cos∠CPN的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,拋物線y=x2+bx+c經過點A(2,﹣3)與C(0,﹣3),與x軸負半軸的交點為B.
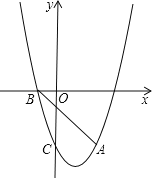
(1)求拋物線的解析式與點B坐標;
(2)若點D在x軸上,使△ABD是等腰三角形,求所有滿足條件的點D的坐標;
(3)點M在拋物線上,點N在拋物線的對稱軸上,若以A、B、M、N為頂點的四邊形是平行四邊形,其中AB∥MN,請直接寫出所有滿足條件的點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年4月23日是中國人民解放軍海軍成立70周年紀念日,屆時將在青島舉行盛大的多國海軍慶祝活動.為此我國海軍進行了多次軍事演習.如圖,在某次軍事演習時,艦艇A發現在他北偏東22°方向上有不明敵艦在指揮中心O附近徘徊,快速報告給指揮中心,此時在艦艇A正西方向50海里處的艦艇B接到返回指揮中心的行動指令,艦艇B迅速趕往在他北偏東60°方向的指揮中心處,艦艇B的速度是80海里/小時,請根據以上信息,求艦艇B到達指揮中心O的時間.(結果精確到0.1小時,參考數據:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
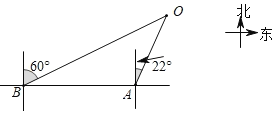
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC看,∠BAC=90°,AC=12,AB=10,D是AC上一個動點,以AD為直徑的⊙O交BD于E,則線段CE的最小值是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 點D在邊AC上(不與A,C重合),連結BD,F為BD中點.
. 點D在邊AC上(不與A,C重合),連結BD,F為BD中點.
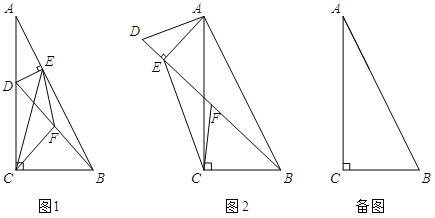
(1)若過點D作DE⊥AB于E,連結CF、EF、CE,如圖1.設![]() ,則k= ;
,則k= ;
(2)若將圖1中的△ADE繞點A旋轉,使得D、E、B三點共線,點F仍為BD中點,如圖2所示.求證:BE-DE=2CF;
(3)若BC=6,點D在邊AC的三等分點處,將線段AD繞點A旋轉,點F始終為BD中點,求線段CF長度的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com