
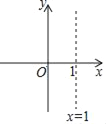
【題目】在平面直角坐標系中,拋物線y=x2﹣2x+c(c為常數)的對稱軸如圖所示,且拋物線過點C(0,c).
(1)當c=﹣3時,點(x1,y1)在拋物線y=x2﹣2x+c上,求y1的最小值;
(2)若拋物線與x軸有兩個交點,自左向右分別為點A、B,且OA=![]() OB,求拋物線的解析式;
OB,求拋物線的解析式;
(3)當﹣1<x<0時,拋物線與x軸有且只有一個公共點,求c的取值范圍.
【答案】(1)-4(2)y=x2﹣2x+![]() 或y=x2﹣2x﹣8(3)當﹣3<c<0時,拋物線與x軸有且只有一個公共點
或y=x2﹣2x﹣8(3)當﹣3<c<0時,拋物線與x軸有且只有一個公共點
【解析】
(1)根據二次函數的性質,求出頂點的縱坐標即可解決問題;
(2)分兩種情形①當點A、B都在原點的右側時,如解圖1,②當點A在原點的左側,點B在原點的右側時,如解圖2,分別求解即可;
(3)把問題轉化為不等式即可解決問題;
(1)當c=﹣3時,拋物線為y=x2﹣2x﹣3,
∴拋物線開口向上,有最小值,
∴y最小值=![]() =﹣4,
=﹣4,
∴y1的最小值為﹣4;
(2)拋物線與x軸有兩個交點,
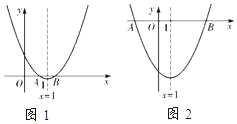
①當點A、B都在原點的右側時,如解圖1,
設A(m,0),
∵OA=![]() OB,
OB,
∴B(2m,0),
∵二次函數y=x2﹣2x+c的對稱軸為x=1,
由拋物線的對稱性得1﹣m=2m﹣1,解得m=![]() ,
,
∴A(![]() ,0),
,0),
∵點A在拋物線y=x2﹣2x+c上,
∴0=![]() ﹣
﹣![]() +c,解得c=
+c,解得c=![]() ,
,
此時拋物線的解析式為y=x2﹣2x+![]() ;
;
②當點A在原點的左側,點B在原點的右側時,如解圖2,
設A(﹣n,0),
∵OA=![]() OB,且點A、B在原點的兩側,
OB,且點A、B在原點的兩側,
∴B(2n,0),
由拋物線的對稱性得n+1=2n﹣1,
解得n=2,
∴A(﹣2,0),
∵點A在拋物線y=x2﹣2x+c上,
∴0=4+4+c,解得c=﹣8,
此時拋物線的解析式為y=x2﹣2x﹣8,
綜上,拋物線的解析式為y=x2﹣2x+![]() 或y=x2﹣2x﹣8;
或y=x2﹣2x﹣8;
(3)∵拋物線y=x2﹣2x+c與x軸有公共點,
∴對于方程x2﹣2x+c=0,判別式b2﹣4ac=4﹣4c≥0,
∴c≤1.
當x=﹣1時,y=3+c;當x=0時,y=c,
∵拋物線的對稱軸為x=1,且當﹣1<x<0時,拋物線與x軸有且只有一個公共點,
∴3+c>0且c<0,解得﹣3<c<0,
綜上,當﹣3<c<0時,拋物線與x軸有且只有一個公共點.


科目:初中數學 來源: 題型:
【題目】某市為創建全國文明城市,開展“美化綠化城市”活動,計劃經過若干年使城區綠化總面積新增360萬平方米.自2013年初開始實施后,實際每年綠化面積是原計劃的1.6倍,這樣可提前4年完成任務.
(1)問實際每年綠化面積多少萬平方米?
(2)為加大創城力度,市政府決定從2016年起加快綠化速度,要求不超過2年完成,那么實際平均每年綠化面積至少還要增加多少萬平方米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】通過課本上對函數的學習,我們積累了一定的經驗,下表是一個函數的自變量![]() 與函數值
與函數值![]() 的部分對應值,請你借鑒以往學習函數的經驗,探究下列問題:
的部分對應值,請你借鑒以往學習函數的經驗,探究下列問題:
| … | 0 | 1 | 2 | 3 | 4 | 5 | … |
| … | 6 | 3 | 2 | 1.5 | 1.2 | 1 | … |
(1)當![]() 時,
時,![]() ;
;
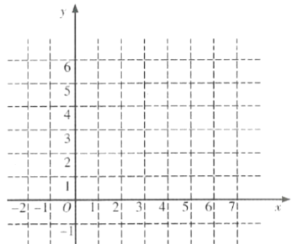
(2)根據表中數值描點![]() ,并畫出函數圖象;
,并畫出函數圖象;
(3)觀察畫出的圖象,寫出這個函數的一條性質: .
查看答案和解析>>
科目:初中數學 來源: 題型:
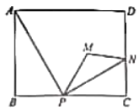
【題目】如圖,在矩形ABCD中,已知![]() ,
,![]() ,點P是邊BC上一動點(點P不與點B,C重合),連接AP,作點B關于直線AP的對稱點M,連接MP,作
,點P是邊BC上一動點(點P不與點B,C重合),連接AP,作點B關于直線AP的對稱點M,連接MP,作![]() 的角平分線交邊CD于點N.則線段MN的最小值為_______________
的角平分線交邊CD于點N.則線段MN的最小值為_______________
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2017河北24題10分)如圖,直角坐標系![]() 中,
中,![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 與
與![]() 軸及直線
軸及直線![]() 分別交于點
分別交于點![]() ,
,![]() ,點
,點![]() ,
,![]() 關于
關于![]() 軸對稱,連接
軸對稱,連接![]() .
.
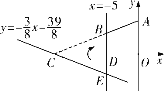
(1)求點![]() ,
,![]() 的坐標及直線
的坐標及直線![]() 的解析式;
的解析式;
(2)設面積的和![]() ,求
,求![]() 的值;
的值;
(3)在求(2)中![]() 時,嘉琪有個想法:“將
時,嘉琪有個想法:“將![]() 沿
沿![]() 軸翻折到
軸翻折到![]() 的位置,而
的位置,而![]() 與四邊形
與四邊形![]() 拼接后可看成
拼接后可看成![]() ,這樣求
,這樣求![]() 便轉化為直接求
便轉化為直接求![]() 的面積不更快捷嗎?”但大家經反復驗算,發現
的面積不更快捷嗎?”但大家經反復驗算,發現![]() ,請通過計算解釋他的想法錯在哪里.
,請通過計算解釋他的想法錯在哪里.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線L: ![]() (常數t>0)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線
(常數t>0)與x軸從左到右的交點為B,A,過線段OA的中點M作MP⊥x軸,交雙曲線![]() 于點P,且OA·MP=12.
于點P,且OA·MP=12.
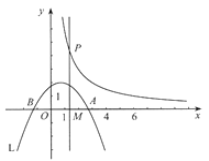
(1)求k值;
(2)當t=1時,求AB長,并求直線MP與L對稱軸之間的距離;
(3)把L在直線MP左側部分的圖象(含與直線MP的交點)記為G,用t表示圖象G最高點的坐標;
(4)設L與雙曲線有個交點的橫坐標為x0,且滿足4≤x0≤6,通過L位置隨t變化的過程,直接寫出t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知點A(5,3),點B(﹣3,3),過點A的直線y=![]() x+m(m為常數)與直線x=1交于點P,與x軸交于點C,直線BP與x軸交于點D.
x+m(m為常數)與直線x=1交于點P,與x軸交于點C,直線BP與x軸交于點D.
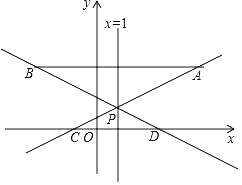
(1)求點P的坐標;
(2)求直線BP的解析式,并直接寫出△PCD與△PAB的面積比;
(3)若反比例函數![]() (k為常數且k≠0)的圖象與線段BD有公共點時,請直接寫出k的最大值或最小值.
(k為常數且k≠0)的圖象與線段BD有公共點時,請直接寫出k的最大值或最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據衢州市統計局發布的統計數據顯示,衢州市近5年國民生產總值數據如圖1所示,2016年國民生產總值中第一產業、第二產業、第三產業所占比例如圖2所示。
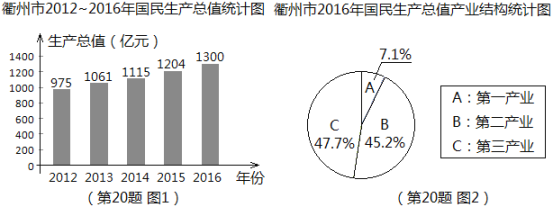
請根據圖中信息,解答下列問題:
(1)求2016年第一產業生產總值(精確到1億元);
(2)2016年比2015年的國民生產總值增加了百分之幾(精確到1%)?
(3)若要使2018年的國民生產總值達到1573億元,求2016年至2018年我市國民生產總值平均年增長率(精確到1%)。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com