
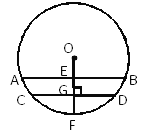
【題目】如圖,圓柱形水管內原有積水的水平面寬CD=10cm,水深GF=1cm,若水面上升1cm(EG=1cm),則此時水面寬AB為多少?
【答案】AB=![]()
【解析】試題分析:
試題解析:連接OA、OC.設 O的半徑是R,則OG=R-1,OE=R-2.根據垂徑定理,得CG=5.在直角三角形OCG中,根據勾股定理求得R的值,再進一步在直角三角形OAE中,根據勾股定理求得AE的長,從而再根據垂徑定理即可求得AB的長.
試題解析:如圖所示,
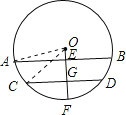
連接OA、OC.
設O的半徑是R,則OG=R1,OE=R2.
∵OF⊥CD,
∴CG=![]() CD=5cm.
CD=5cm.
在直角三角形COG中,根據勾股定理,得
R2=52+(R1)2,
解,得R=13.
在直角三角形AOE中,根據勾股定理,得
AE=![]() =
=![]() =
=![]() =
=![]() cm.
cm.
根據垂徑定理,得AB=2AE=![]() (cm).
(cm).
則此時水面寬AB為![]() cm.
cm.


科目:初中數學 來源: 題型:
【題目】為了解某班學生每天使用零花錢的情況,小紅隨機調查了15名同學,結果如下表:
每天使用零花錢 | 1 | 2 | 3 | 5 | 6 |
人 數 | 2 | 5 | 4 | 3 | 1 |
則這15名同學每天使用零花錢的眾數和中位數分別是( )
A.3,3
B.2,3
C.2,2
D.3,5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,屬于假命題的是( )
A. 三角形三個內角和等于180° B. 兩直線平行,同位角相等
C. 同位角相等,兩直線平行 D. 相等的兩個角是對頂角
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張勤同學的父母在外打工,家中只有年邁多病的奶奶.星期天早上,李老師從家中出發步行前往張勤家家訪.6分鐘后,張勤從家出發騎車到相距1200米的藥店給奶奶買藥,停留14分鐘后以相同的速度按原路返回,結果與李老師同時到家.張勤家、李老師家、藥店都在東西方向筆直大路上,且藥店在張勤家與李老師家之間.在此過程中設李老師出發t(0≤t≤32)分鐘后師生二人離張勤家的距離分別為S1、S2.S與t之間的函數關系如圖所示,請你解答下列問題:
(1)李老師步行的速度為 ;
(2)求S2與t之間的函數關系式,并在如圖所示的直角坐標系中畫出其函數圖象;
(3)張勤出發多長時間后在途中與李老師相遇?

查看答案和解析>>
科目:初中數學 來源: 題型:
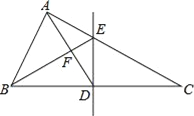
【題目】如圖,在△ABC中,BC的垂直平分線分別交BC,AC于點D,E,BE交AD于點F,AB=AD.
(1)判斷△FDB與△ABC是否相似,并說明理由.
(2)AF與DF相等嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=kx+b交x軸于點A,交y軸于點B,線段AB的中點E的坐標為(2,1).
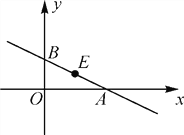
(1)求k,b的值;
(2)P為直線AB上一點,PC⊥x軸于點C,PD⊥y軸于點D,若四邊形PCOD為正方形,求點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com