【題目】日歷上的規律：表格是2020年元月的日歷，圖中的陰影區域是在日歷中選取的一塊九宮格.
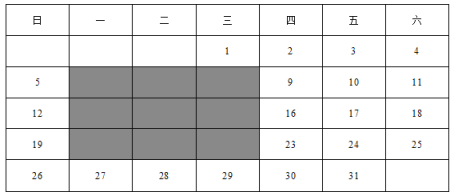
（1）九宮格中，四個角的四個數之和與九宮格中央那個數有什么關系？
（2）請你自選一塊九宮格進行計算，看四個角上的四個數之和與九宮格中央那個數是否還有這種關系？
（3）試說明原理.
【答案】（1）四個角上的四個數之和等于九宮格中央這個數的4倍；（2）有；（3）詳見解析.
【解析】
（1）先分別找出四個角的四個數與九宮格中央所代表的數，然后通過計算即可得出結論；
（2）根據上圖隨意找出九個數然后計算，觀察是否符合結論；
（3）設九宮格中央這個數為
，那么上角兩個數分別為
、
，下角兩個數分別為
、
，然后通過計算驗證即可.
解：（1）根據題意可知四個角的四個數與九宮格中央所代表的數分別為：6,22,8,20與14
則
.
即四個角上的四個數之和等于九宮格中央這個數的4倍；
（2）取如下圖的數據
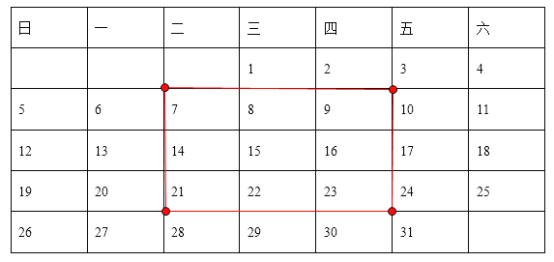
則有
即四個角上的四個數之和等于九宮格中央這個數的4倍；
（3）設九宮格中央這個數為，那么上角兩個數分別為、，
下角兩個數分別為、，
四個數的和：
.
發散思維新課堂系列答案科目：初中數學 來源： 題型：
【題目】如圖，一次函數
（k≠0）的圖象與反比例函數
（m≠0，x＜0）的圖象交于點A（-3，1）和點C，與y軸交于點B，△AOB的面積是6．
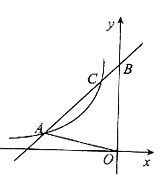
（1）求一次函數與反比例函數的解析式；
（2）求 sin∠ABO的值；
（3）當x＜0時，比較
與
的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】若二次函數y=ax2+bx﹣4的圖象開口向上，與x軸的交點為（4，0）、（﹣2，0），則當x1=﹣1，x2=2時，對應的函數值y1和y2的大小關系為（ ）
A. y1＞y2 B. y1=y2 C. y1＜y2 D. 不確定
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，DE是△ABC的中位線，F是DE的中點，CF的延長線交AB于點G，若△CEF的面積為18cm2，則S△DGF等于（ ）
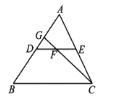
A.4cm2B.5cm2C.6cm2D.7 cm2
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AB=BC，對角線BD平分ABC，P是BD上一點，過點P作PM^AD，PN^CD，垂足分別為M、N。
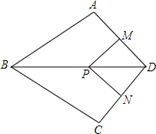
（1）求證：ADB=CDB；
（2）若ADC=90°，求證：四邊形MPND是正方形。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點P是正方形ABCD對角線AC上一動點，點E在射線BC上，且PB＝PE，連接PD，O為AC中點．
(1)如圖1，當點P在線段AO上時，試猜想PE與PD的數量關系和位置關系，不用說明理由；
(2)如圖2，當點P在線段OC上時，(1)中的猜想還成立嗎？請說明理由；
(3)如圖3，當點P在AC的延長線上時，請你在圖3中畫出相應的圖形(尺規作圖，保留作圖痕跡，不寫作法)，并判斷(1)中的猜想是否成立？若成立，請直接寫出結論；若不成立，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】關于三角函數有如下的公式：
sin（α+β）=sinαcosβ+cosαsinβ①
cos（α+β）=cosαcosβ﹣sinαsinβ②
tan（α+β）=
③
利用這些公式可將某些不是特殊角的三角函數轉化為特殊角的三角函數來求值，如：
tan105°=tan（45°+60°）=
=﹣（2+
）．
根據上面的知識，你可以選擇適當的公式解決下面的實際問題：
如圖，直升飛機在一建筑物CD上方A點處測得建筑物頂端D點的俯角α=60°，底端C點的俯角β=75°，此時直升飛機與建筑物CD的水平距離BC為42m，求建筑物CD的高．
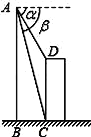
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD中，AC，BD相交于點O，O是AC的中點，AD//BC，AC=8,BD=6.
（1）求證：四邊形ABCD是平行四邊形；
（2）若AC⊥BD，求□ABCD的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
