
【題目】如圖,在直角坐標系中,直線![]() 與x軸,y軸分別交于點A,B,點
與x軸,y軸分別交于點A,B,點![]() 在第一象限內,連結
在第一象限內,連結![]() ,
,![]() ,
,![]() .動點P在
.動點P在![]() 上從點A向終點B勻速運動,同時,動點Q在
上從點A向終點B勻速運動,同時,動點Q在![]() 上從點C向終點O勻速運動,它們同時到達終點,連結
上從點C向終點O勻速運動,它們同時到達終點,連結![]() 交
交![]() 于點D.
于點D.
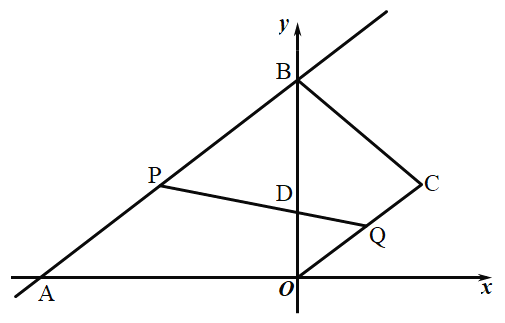
(1)求點B的坐標和a的值;
(2)當點Q運動到![]() 中點時,連結
中點時,連結![]() ,求
,求![]() 的面積;
的面積;
(3)作![]() 交直線
交直線![]() 于點R.
于點R.
①當![]() 為等腰三角形時,求
為等腰三角形時,求![]() 的長度;
的長度;
②記![]() 交
交![]() 于點E,連結
于點E,連結![]() ,則
,則![]() 的最小值為__________.(直接寫出答案)
的最小值為__________.(直接寫出答案)
【答案】(1)![]() ,
,![]() ;(2)6;(3)①
;(2)6;(3)①![]() 或
或![]() 或
或![]() ;②
;②![]()
【解析】
(1)根據![]() 令
令![]() 求算B的坐標;再根據
求算B的坐標;再根據![]() ,得出OC的斜率和AB的斜率相等進行求算;
,得出OC的斜率和AB的斜率相等進行求算;
(2)延長PQ與x軸交于G點,根據題意知:P點運動速度是Q點的兩倍,得出點Q運動到![]() 中點時,P運動到AB中點,求出PQ的直線解析式從而得出G點的坐標,再根據
中點時,P運動到AB中點,求出PQ的直線解析式從而得出G點的坐標,再根據![]() 求算即可;
求算即可;
(3)①![]() ,設AP=2t,CQ=t,易得:
,設AP=2t,CQ=t,易得:![]()
![]() ,表示出P、Q、R的坐標,再根據
,表示出P、Q、R的坐標,再根據![]() 為等腰三角形分類討論即可;
為等腰三角形分類討論即可;
②根據①中P、Q的點坐標表示出PQ的函數解析式,從而求算D點坐標,再表示出E點坐標,根據距離公式表示出DE的長度,配方成頂點式求算最小值.
(1)∵直線![]() 與x軸,y軸分別交于點A,B
與x軸,y軸分別交于點A,B
∴![]()
又∵![]() ,點
,點![]()
∴![]() 即
即![]()
∴![]()
綜上所述:B點坐標為![]() ,
,![]() ;
;
(2)延長PQ與x軸交于G點:
由(1)知:AB=10,OC=5, 根據題意知:P點運動速度是Q點的兩倍
∴點Q運動到![]() 中點時,P運動到AB中點
中點時,P運動到AB中點
∴![]()
設PQ的解析式為:![]() ,代入得:
,代入得:
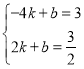 解得:
解得: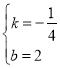
∴PQ的解析式為:![]()
∴![]()
∴![]()
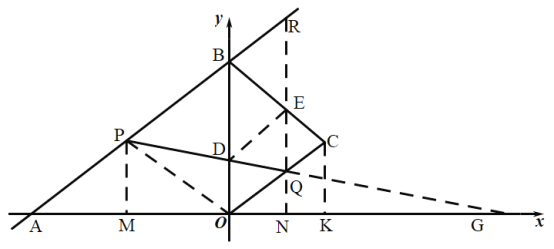
(3)①作![]()
根據題意知:P點運動速度是Q點的兩倍,設AP=2t,CQ=t
易得:![]()
∴![]() ,代入得:
,代入得:
![]()
∴![]()
當![]() 時:根據三線合一知:
時:根據三線合一知:
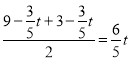 解得:
解得:![]()
∴CQ為![]() ;
;
當![]() 時:通過距離公式得:
時:通過距離公式得:
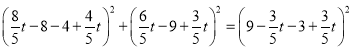 ,解得:
,解得:![]() (舍)
(舍)
∴CQ為![]() ;
;
當![]() 時,通過距離公式得:
時,通過距離公式得:
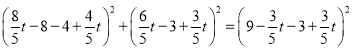 ,解得:
,解得:![]() (舍)
(舍)
∴CQ為![]()
綜上所述:當![]() 為等腰三角形時,求
為等腰三角形時,求![]() 的長
的長![]() 或
或![]() 或
或![]() ;
;
②設PQ的解析式為:![]() 代入P、Q:
代入P、Q:
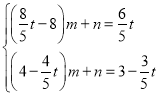 解得:
解得: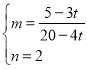
∴![]()
設BC的解析式為:![]() ,代入B、C得:
,代入B、C得:
![]() 解得
解得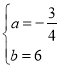
∴BC的解析式為:![]()
∴![]()
∴由距離公式得: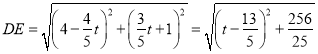
∴當![]() 時,DE有最小值為
時,DE有最小值為![]()
綜上所述:DE最小值為![]()


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:
【題目】只有1和它本身兩個因數且大于1的正整數叫做素數.我國數學家陳景潤哥德巴赫猜想的研究中取得了世界領先的成果.哥德巴赫猜想是“每個大于2的偶數都表示為兩個素數的和”,如10=3+7.
(1)從7,11,13,17這4個素數中隨機抽取一個,則抽到的數是11的概率是_____;
(2)從7,11,13,17這4個素數中隨機抽取1個數,再從余下的3個數中隨機抽取1個數,用畫樹狀圖或列表的方法,求抽到的兩個素數之和等于24的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1是一座立交橋的示意圖(道路寬度忽略不計),A為入口,F,G為出口,其中直行道為AB,CG,EF,且AB=CG=EF;彎道為以點O為圓心的一段弧,且所對的圓心角均為90°.甲、乙兩車由A口同時駛入立交橋,均以8m/s的速度行駛,從不同出口駛出,其間兩車到點O的距離y(m)與時間x(s)的對應關系如圖2所示,結合題目信息,下列說法錯誤的是( )
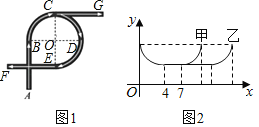
A.立交橋總長為168 m
B.從F口出比從G口出多行駛48m
C.甲車在立交橋上共行駛11 s
D.甲車從F口出,乙車從G口出
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,點
點,點![]() 在直線
在直線![]() 上,橫坐標為
上,橫坐標為![]() .
.
(1)確定二次函數![]() 的解析式;
的解析式;
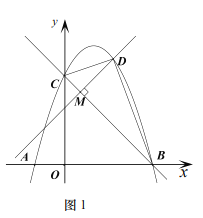
(2)如圖1,![]() 時,
時,![]() 交二次函數
交二次函數![]() 的圖象于點
的圖象于點![]() 的面積記作
的面積記作![]() 為何值時
為何值時![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
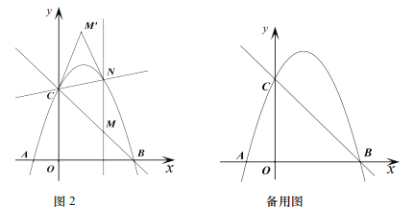
(3)如圖2,過點![]() 作
作![]() 軸的平行線交二次函數
軸的平行線交二次函數![]() 的圖象于點
的圖象于點![]() 點
點![]() 與點
與點![]() 關于直線
關于直線![]() 對稱是否存在點
對稱是否存在點![]() 使四邊形
使四邊形![]() 為菱形,若存在直接寫出
為菱形,若存在直接寫出![]() 的值;若不存在請說明理由.
的值;若不存在請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
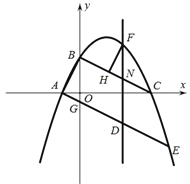
【題目】如圖所示,在平面直角坐標系中,拋物線![]() 與y軸交于點B,與x軸交于點A,C(點A在點C的左側),A(-1,0),C(4,0),連接AB,BC,點
與y軸交于點B,與x軸交于點A,C(點A在點C的左側),A(-1,0),C(4,0),連接AB,BC,點![]() 為y軸負半軸上的一點,連接AG并延長交拋物線于點E,點D為線段AE上的一個動點,過點D作y軸的平行線交拋物線于點F,與線段BC交于點N.
為y軸負半軸上的一點,連接AG并延長交拋物線于點E,點D為線段AE上的一個動點,過點D作y軸的平行線交拋物線于點F,與線段BC交于點N.
(1)求拋物線的表達式及直線BC的表達式;
(2)在點D運動的過程中,當FN的值最大時,在線段BC上是否存在一點H,使得FNH與ABC相似,如果存在,求出此時H點的坐標;
(3)當DF=4時,連接DC,四邊形ABCD先向上平移一定單位長度后,使點D落在x軸上,然后沿x軸向左平移n(1n4)個單位長度,用含n的表達式表示平移后的四邊形與原四邊形重疊部分的面積S(直接寫出結果).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果商場經銷一種高檔水果,原價每千克25元,連續兩次漲價后每千克水果現在的價格為36元.
(1)若每次漲價的百分率相同.求每次漲價的百分率;
(2)若進價不變,按現價售出,每千克可獲利15元,但該水果出現滯銷,商場決定降價m元出售,同時把降價的幅度m控制在![]() 的范圍,經市場調查發現,每天銷售量
的范圍,經市場調查發現,每天銷售量![]() (千克)與降價的幅度m(元)成正比例,且當
(千克)與降價的幅度m(元)成正比例,且當![]() 時,
時,![]() . 求
. 求![]() 與 m的函數解析式;
與 m的函數解析式;
(3)在(2)的條件下,若商場每天銷售該水果盈利![]() 元,為確保每天盈利
元,為確保每天盈利![]() 最大,該水果每千克應降價多少元?
最大,該水果每千克應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“扶貧攻堅”活動中,某單位計劃選購甲,乙兩種物品慰問貧困戶.已知甲物品的單價比乙物品的單價高10元,若用500元單獨購買甲物品與450元單獨購買乙物品的數量相同.求甲,乙兩種物品的單價各多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知⊙O的半徑為3,A為圓內一定點,AO=1,P為圓上一動點,以AP為邊作等腰△APQ,AP=PQ,∠APQ=120°,則OQ的最大值為( )
A.1+3![]() B.1+2
B.1+2![]() C.3+
C.3+![]() D.3
D.3![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com