
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 在邊
在邊![]() 上,以
上,以![]() 為圓心,
為圓心,![]() 為半徑的弧經過點
為半徑的弧經過點![]() 是弧
是弧![]() 上一個動點.
上一個動點.
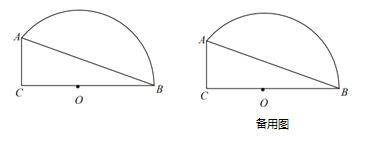
![]() 求半徑
求半徑![]() 的長;
的長;
![]() 如果點
如果點![]() 是弧
是弧![]() 的中點,聯結
的中點,聯結![]() ,求
,求![]() 的正切值;
的正切值;
![]() 如果
如果![]() 平分
平分![]() ,延長
,延長![]() 交于點
交于點![]() ,求線段
,求線段![]() 的長.
的長.
【答案】(1)9;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據勾股定理得到AB=![]() =12
=12![]() ,如圖1,過O作OH⊥AB于H,根據相似三角形的性質即可得到結論;
,如圖1,過O作OH⊥AB于H,根據相似三角形的性質即可得到結論;
(2)如圖2,連接OP交AB于H,根據垂徑定理得到OP⊥AB,AH=BH=![]() AB=6
AB=6![]() ,得到PH=9-3=6,根據圓周角定理得到∠PCB=∠PBA,根據三角函數的定義即可得到結論;
,得到PH=9-3=6,根據圓周角定理得到∠PCB=∠PBA,根據三角函數的定義即可得到結論;
(3)如圖3,過A作AE⊥BD于E,連接CP,根據角平分線的性質得到AE=AC=4![]() ,根據相似三角形的性質得到AD=
,根據相似三角形的性質得到AD=![]() ,根據全等三角形的性質得到BE=BC=16,根據勾股定理和三角形的面積公式即可得到結論.
,根據全等三角形的性質得到BE=BC=16,根據勾股定理和三角形的面積公式即可得到結論.
解:![]() )∵Rt△ABC中,∠ACB=90°,AC=4
)∵Rt△ABC中,∠ACB=90°,AC=4![]() ,BC=16,
,BC=16,
∴AB=![]() =12
=12![]() ,
,
如圖1,過O作OH⊥AB于H,
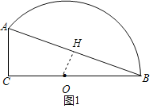
則BH=![]() AB=6
AB=6![]() ,
,
∵∠BHO=∠ACB=90°,∠B=∠B,
∴△BHO∽△BCA,
∴![]()
∴![]()
∴OB=9;
(2) 如圖2,連接OP交AB于H,連結![]() ,交
,交![]() 于點
于點![]() ,
,
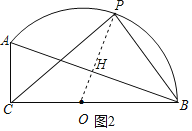
![]() 是弧
是弧![]() 的中點,
的中點,![]() 過圓心
過圓心
![]() , AH=BH=
, AH=BH=![]() AB=6
AB=6![]() ,
,
在Rt△BHO中,OH=![]() =
=![]() =3,
=3,
∴PH=9-3=6,
∵點P是弧AB的中點,
∴弧AP=弧PB,
∴∠PCB=∠PBA,
∴∠PCB的正切值=∠PBA的正切值=![]() =
=![]() ;
;
![]() 如圖3,過A作AE⊥BD于E,連接CP,
如圖3,過A作AE⊥BD于E,連接CP,
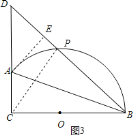
∵BA平分∠PBC,AC⊥BC,
∴AE=AC=4![]() ,
,
∵∠AED=∠ACB=90°,∠D=∠D,
∴△ADE∽△BDC,
∴![]() ,
,
設DE=x,
∴![]() ,
,
∴AD=![]()
在Rt△ACB與Rt△AEB中,![]()
∴Rt△ACB≌Rt△AEB(HL),
∴BE=BC=16,
∵CD2+BC2=BD2,
∴(4![]() +
+![]() )2+162=(16+x)2,
)2+162=(16+x)2,
解得:x=![]()
∴AD=![]() ,BD=16+
,BD=16+![]() =
=![]() ,
,
∴CD=![]()
∵BC是⊙的直徑,
∴CP⊥BD,
∴CP=![]() =
=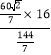 =
= ![]()
∴PD=![]() =
=![]()


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB于H,G為⊙O上一點,連接AG交CD于K,在CD的延長線上取一點E,使EG=EK,EG的延長線交AB的延長線于F.
(1)求證:EF是⊙O的切線;
(2)連接DG,若AC∥EF時.
①求證:△KGD∽△KEG;
②若cosC=![]() ,AK=
,AK=![]() ,求BF的長.
,求BF的長.
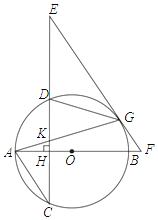
查看答案和解析>>
科目:初中數學 來源: 題型:
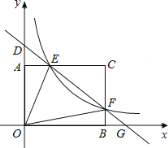
【題目】如圖,矩形AOBC的頂點坐標分別為A(0,3),O(0,0),B(4,0),C(4,3),動點F在邊BC上(不與B.C重合),過點F的反比例函數y=![]() 的圖象與邊AC交于點E,直線EF分別與y軸和x軸相交于點D和G.給出下列命題:①若k=4,則△OEF的面積為
的圖象與邊AC交于點E,直線EF分別與y軸和x軸相交于點D和G.給出下列命題:①若k=4,則△OEF的面積為![]() ;②若k=
;②若k=![]() ,則點C關于直線EF的對稱點在x軸上;③滿足題設的k的取值范圍是0<k≤12;④若DEEG=
,則點C關于直線EF的對稱點在x軸上;③滿足題設的k的取值范圍是0<k≤12;④若DEEG=![]() ,則k=1.其中正確的命題的序號是____________(填序號).
,則k=1.其中正確的命題的序號是____________(填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了安全,交通部門一再提醒司機:請勿超速!同時,進一步完善各類監測系統,如圖,在松銅公路某直線路段MN內限速60千米/小時,為了檢測車輛是否超速,在公路MN旁設立了測速點C,從測速點C測得一小車從點A到達點B行駛了3秒鐘,已知∠CAN=45°,∠CBN=60°,BC=120米.
(1)求測速點C到該段公路的距離;
(2)請你通過計算判斷此車是否超速,(結果精確到0.1m/s)(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中數學 來源: 題型:
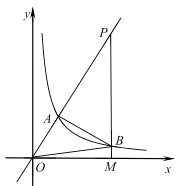
【題目】如圖,反比例函數![]() 的圖象與正比例函數
的圖象與正比例函數![]() 圖象交于點
圖象交于點![]() ,且點
,且點![]() 的橫坐標為2.
的橫坐標為2.
(1)求反比例函數的表達式;
(2)若射線![]() 上有一點
上有一點![]() ,且
,且![]() ,過點
,過點![]() 作
作![]() 與
與![]() 軸垂直,垂足為
軸垂直,垂足為![]() ,交反比例函數圖象于點
,交反比例函數圖象于點![]() ,連接
,連接![]() ,
,![]() ,請求出
,請求出![]() 的面積.
的面積.
(3)定義:橫縱坐標均為整數的點稱為“整點”.在(2)的條件下,請探究邊![]() ,
,![]() 與反比例函數圖象圍成的區域內(不包括邊界)“整點”的個數.
與反比例函數圖象圍成的區域內(不包括邊界)“整點”的個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一條直線與反比例函數![]() 的圖像交于
的圖像交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,
點,![]() 軸,垂足為
軸,垂足為![]() .
.
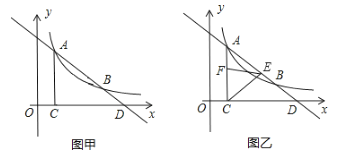
(1)如圖甲,求反比例函數的解析式與![]() 點的坐標;
點的坐標;
(2)如圖乙,若點![]() 在線段
在線段![]() 上運動,連接
上運動,連接![]() ,作
,作![]() ,
,![]() 交
交![]() 于
于![]() 點.試說明
點.試說明![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某建設工地一個工程有大量的沙石需要運輸.建設公司車隊有載重量為8噸和10噸的卡車共12輛,全部車輛一次能運輸110噸沙石
(1)求建設公司車隊載重量為8噸和10噸的卡車各有多少輛?
(2)隨著工程的進展,車隊需要一次運輸沙石超過160噸,為了完成任務,準備新增購這兩種卡車共6輛,車隊最多新購買載重量為8噸的卡車多少輛?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場試銷一種成本為![]() 元/件的T 恤,規定試銷期間單價不低于成本單價,又獲利不得高于
元/件的T 恤,規定試銷期間單價不低于成本單價,又獲利不得高于![]() ,經試銷發現,銷售量
,經試銷發現,銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元/件)符合一次函數
(元/件)符合一次函數![]() ,且
,且![]() 時,
時,![]() ;
;![]() 時,
時,![]() .
.
(1)寫出銷售單價![]() 的取值范圍;
的取值范圍;
(2)求出一次函數![]() 的解析式;
的解析式;
(3)若該商場獲得利潤為![]() 元,試寫出利潤
元,試寫出利潤![]() 與銷售單價
與銷售單價![]() 之間的關系式,銷售單價定為多少時,商場可獲得最大利潤,最大利潤是多少?
之間的關系式,銷售單價定為多少時,商場可獲得最大利潤,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
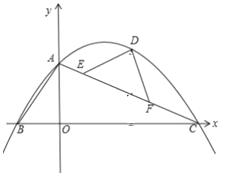
【題目】如圖,平面直角坐標系中,O為坐標原點,直線y=﹣![]() x+4交x軸于點C,交y軸于點A,過A、C兩點的拋物線y=ax2+bx+4交x軸負半軸于點B,且tan∠BAO=
x+4交x軸于點C,交y軸于點A,過A、C兩點的拋物線y=ax2+bx+4交x軸負半軸于點B,且tan∠BAO=![]() .
.
(1)求拋物線的解析式;
(2)已知E、F是線段AC上異于A、C的兩個點,且AE<AF,EF=2![]() ,D為拋物線上第一象限內一點,且DE=DF,設點D的橫坐標為m,△DEF的面積為S,求S與m的函數關系式(不要求寫出自變量m的取值范圍);
,D為拋物線上第一象限內一點,且DE=DF,設點D的橫坐標為m,△DEF的面積為S,求S與m的函數關系式(不要求寫出自變量m的取值范圍);
(3)在(2)的條件下,當∠EDF=90°時,連接BD,P為拋物線上一動點,過P作PQ⊥BD交線段BD于點Q,連接EQ.設點P的橫坐標為t,求t為何值時,PE=QE.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com