
【題目】如圖,直線l:y=﹣![]() x+2與x軸、y軸分別交于A、B兩點,動點M從點A以每秒1個單位的速度沿x軸向左移動.
x+2與x軸、y軸分別交于A、B兩點,動點M從點A以每秒1個單位的速度沿x軸向左移動.
(1)求A、B兩點的坐標;
(2)將直線l向上平移4個單位后得到直線l',交y軸于點C.求直線l′的函數表達式;
(3)設點M的移動時間為t,當t為何值時,△COM≌△AOB,并求出此時點M的坐標.
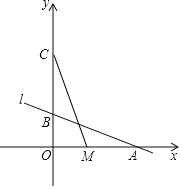
【答案】(1)A(6,0)、B(0,2);(2)![]() ;(3)當t=4或8時,△COM≌△AOB,此時M(2,0)或(﹣2,0).
;(3)當t=4或8時,△COM≌△AOB,此時M(2,0)或(﹣2,0).
【解析】
(1)A和B是坐標軸上的點,求A和B的坐標,只需要令x=0,y=0,即可算出.
(2)向上平移4個單位,就是y軸交點縱坐標向上平移4個單位.平移的函數表達式k不變,利用待定系數法可以求出![]() 得表達式.
得表達式.
(3)![]() 和
和![]() 中,OC=OA=6,
中,OC=OA=6,![]() ,要使
,要使![]() ≌
≌![]() ,只需要OB=OM就行.OB=2,當OM=2時,M在y軸左邊時,AM=8,t=8;M在y軸在右邊時,AM=4,t=4.
,只需要OB=OM就行.OB=2,當OM=2時,M在y軸左邊時,AM=8,t=8;M在y軸在右邊時,AM=4,t=4.
解:(1)對于直線l:y=﹣![]() x+2,
x+2,
當x=0時,y=2;當y=0時,x=6,
則A、B兩點的坐標分別為A(6,0)、B(0,2);
(2)設直線l′的函數表達式為y=kx+b,
∵l′∥l,
∴k=﹣![]() ,
,
由題意l′經過點(0,6),
∴b=6,
∴l′的函數表達式為![]() ;
;
(3)∵OC=OA=6,∠AOB=∠COM=90°,
∴當點M在OA上時,OB=OM=2,則△COM≌△AOB,
∴AM=AO﹣OM=4,
∴t=4÷1=4,M(2,0).
當M在x軸的負半軸上時,OM=OB=2,△COM≌△AOB,AM=8,
∴t=8÷1=8,點M(﹣2,0).
故當t=4或8時,△COM≌△AOB,此時M(2,0)或(﹣2,0).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
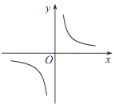
【題目】已知反比例函數 y=![]() 的圖象如圖所示,則二次函數 y =ax 2-2x和一次函數 y=bx+a 在同一平面直角坐標系中的圖象可能是( )
的圖象如圖所示,則二次函數 y =ax 2-2x和一次函數 y=bx+a 在同一平面直角坐標系中的圖象可能是( )
A.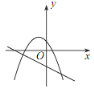 B.
B.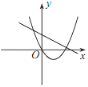 C.
C.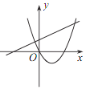 D.
D.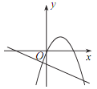
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】成都市天府一南站城市立交橋是成都市政府確定的城建標志性建筑,如圖是立交橋引申出的部分平面圖,測得拉索AB與水平橋面的夾角是37°,拉索DE與水平橋面的夾角是67°,兩拉索頂端的距離AD為2m,兩拉索底端距離BE為10m,請求出立柱AC的長.(參考數據tan37°≈![]() ,sin37°≈
,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan67°≈
,tan67°≈![]() ,sin67°≈
,sin67°≈![]() ,cos67°≈
,cos67°≈![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小麗同學學習了統計知識后,帶領班級“課外活動小組”,隨機調查了某轄區若干名居民的年齡,并將調查數據繪制成圖①和圖②兩幅尚不完整的統計圖.
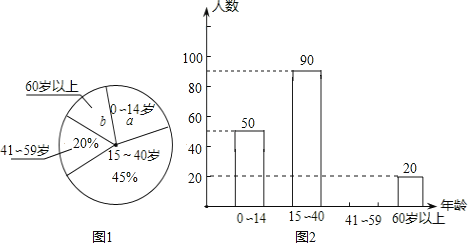
請你根據圖中的信息,解答下列各題:
(1)共抽查了_____名居民的年齡,扇形統計圖中![]() _____,
_____,![]() ______;
______;
(2)補全條形統計圖;
(3)若該轄區居民約有2600人,請你估計年齡在15~59歲的居民人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半徑為5的⊙A中,弦BC,ED所對的圓心角分別是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,則弦BC的弦心距等于 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校初級中學數學興趣小組為了解本校學生年齡情況,隨機調查了本校部分學生的年齡,根據所調查的學生的年齡(單位:歲),繪制出如下的統計圖①和圖②,請根據相關信息,解答下列問題:
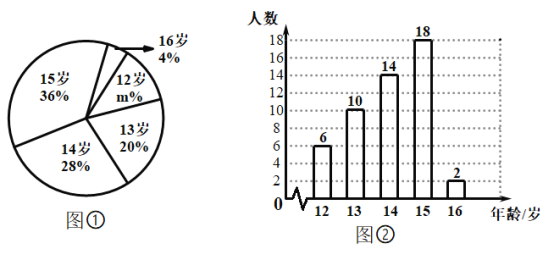
(1)本次接受調查的學生人數為_______,圖①中 ![]() 的值為 ;
的值為 ;
(2)求統計的這組學生年齡數據的平均數、眾數和中位數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 的正方形網格中,每個小正方形的邊長均為1,
的正方形網格中,每個小正方形的邊長均為1,![]() 的三個頂點均在小正方形的頂點上.
的三個頂點均在小正方形的頂點上.
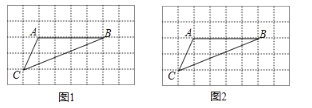
(1)在圖1中畫一個![]() (點
(點![]() 在小正方形的頂點上),使
在小正方形的頂點上),使![]() 的周長等于
的周長等于![]() 的周長,且以
的周長,且以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是軸對稱圖形;
為頂點的四邊形是軸對稱圖形;
(2)在圖2中畫![]() (點
(點![]() 在小正方形的頂點上),使
在小正方形的頂點上),使![]() 的周長等于
的周長等于![]() 的周長,且以
的周長,且以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是中心對稱圖形;
為頂點的四邊形是中心對稱圖形;
(3)直接寫出圖2中四邊形的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=﹣x2+bx+c的圖象經過點A(3,1),點B(0,4).
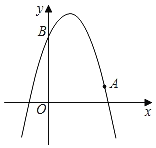
(1)求該二次函數的表達式及頂點坐標;
(2)點C(m,n)在該二次函數圖象上.
①當m=﹣1時,求n的值;
②當m≤x≤3時,n最大值為5,最小值為1,請根據圖象直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
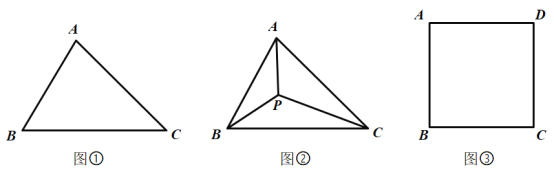
【題目】問題探究
(1)請在圖①的![]() 的邊
的邊![]() 上求作一點
上求作一點![]() ,使
,使![]() 最短;
最短;
(2)如圖②,點![]() 為
為![]() 內部一點,且滿足
內部一點,且滿足![]() .求證:點
.求證:點![]() 到點
到點![]() 、
、![]() 、
、![]() 的距離之和最短,即
的距離之和最短,即![]() 最短;
最短;
問題解決
(3)如圖③,某高校有一塊邊長為400米的正方形草坪![]() ,現準備在草坪內放置一對石凳及垃圾箱在
,現準備在草坪內放置一對石凳及垃圾箱在![]() 點處,使點
點處,使點![]() 到
到![]() 、
、![]() 、
、![]() 三點的距離之和最小,那么是否存在符合條件的點
三點的距離之和最小,那么是否存在符合條件的點![]() ?若存在,請作出點
?若存在,請作出點![]() 的位置,并求出這個最短距離;若不存在,請說明理由.
的位置,并求出這個最短距離;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com