【題目】如圖，以矩形
的頂點
為圓心，線段
長為半徑畫弧，交
邊于
點；再以頂點
為圓心，線段
長為半徑畫弧，交邊于
點，若
，則
、
和
圍成的陰影面積是_____．
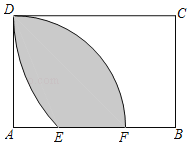
【答案】
【解析】
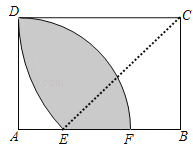
如圖，連接EC，首先證明△BEC是等腰直角三角形，然后根據S陰影＝S矩形ABCD（S矩形ABCDS扇形ADF）（S矩形ABCDS扇形CDES△EBC）＝S扇形ADF＋S扇形CDE＋S△EBCS矩形ABCD計算即可．
解：如圖，連接EC，
∵四邊形ABCD是矩形，
∴AD＝BC＝5，CD＝AB＝EC＝
，∠B＝∠A＝∠DCB＝90°，
∴BE＝
，
∴BC＝BE＝5，
∴∠BEC＝∠BCE＝45°，
∴∠ECD＝45°，
∴S陰影＝S矩形ABCD（S矩形ABCDS扇形ADF）（S矩形ABCDS扇形CDES△EBC），
＝S扇形ADF＋S扇形CDE＋S△EBCS矩形ABCD，
＝
，
＝
，
＝．
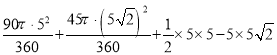故答案為：．
科目：初中數學 來源： 題型：
【題目】一輛客車從甲地出發前往乙地，平均速度v(千米/小時)與所用時間t(小時)的函數關系如圖所示，其中60≤v≤120.
(1)直接寫出v與t的函數關系式；
(2)若一輛貨車同時從乙地出發前往甲地，客車比貨車平均每小時多行駛20千米，3小時后兩車相遇．
①求兩車的平均速度；
②甲、乙兩地間有兩個加油站A、B，它們相距200千米，當客車進入B加油站時，貨車恰好進入A加油站(兩車加油的時間忽略不計)，求甲地與B加油站的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠ACB＝90°，D為AB的中點，以CD為直徑的⊙O分別交AC，BC于點E，F兩點，過點F作FG⊥AB于點G．
（1）試判斷FG與⊙O的位置關系，并說明理由．
（2）若AC＝3，CD＝2.5，求FG的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是半圓O的直徑，點P是BA延長線上一點，PC是⊙O的切線，切點為C，過點B作BD⊥PC交PC的延長線于點D，連接BC．求證：
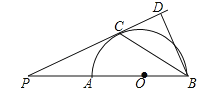
（1）∠PBC=∠CBD；
（2）
=ABBD．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，將一矩形OABC放在直角坐標系中，O為坐標原點，點A在y軸正半軸上，點E是邊AB上的一個動點
不與點A、B重合
，過點E的反比例函數
的圖象與邊BC交于點F
若
的面積為
，且
，求k的值；
若
，
，反比例函數的圖象與邊AB、邊BC交于點E和F，當
沿EF折疊，點B恰好落在OC上，求k的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
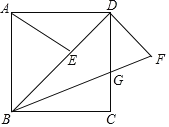
【題目】如圖，在正方形ABCD中，點E是對角線BD上一點，連接AE，將DE繞D點逆時針方向旋轉90°到DF，連接BF，交DC于點G，若DG=3，CG=2，則線段AE的長為__．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在直角三角形ABC中，∠C＝90°，AC＝2，BC＝2
，點O是邊AB上的一個動點，以點O為圓心，OA為半徑作⊙O，與邊AC交于點M．
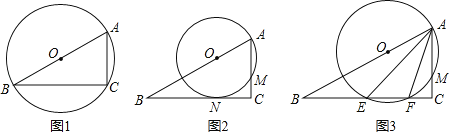
（1）如圖1，當⊙O經過點C時，⊙O的直徑是 ；
（2）如圖2，當⊙O與邊BC相切時，切點為點N，試求⊙O與△ABC重合部分的面積；
（3）如圖3，當⊙O與邊BC相交時，交點為E、F，設CM＝x，就判斷AEAF是否為定值，若是，求出這個定值；若不是，請用含x的代數式表示．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】使用家用燃氣灶燒開同一壺水所需的燃氣量
（單位：
）與旋鈕的旋轉角度
（單位：度）（
）近似滿足函數關系y=ax2+bx+c(a≠0).如圖記錄了某種家用燃氣灶燒開同一壺水的旋鈕角度與燃氣量的三組數據，根據上述函數模型和數據，可推斷出此燃氣灶燒開一壺水最節省燃氣的旋鈕角度約為（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
