
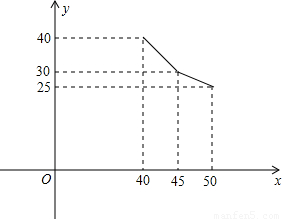
 隨著經濟發展,污染問題日益嚴重.某環保廠家看到這個商機,以200萬元購買了某項空氣凈化產品的生產技術后,再投入280萬元購買生產設備進行該產品的生產.已知生產這種產品的成本價為每件30元,經過市場調研發現,該產品的銷售單價定在40到50元之間較為合理,并且該產品的年銷售量y(萬件)與銷售單價x(元)之間的關系如圖所示.
隨著經濟發展,污染問題日益嚴重.某環保廠家看到這個商機,以200萬元購買了某項空氣凈化產品的生產技術后,再投入280萬元購買生產設備進行該產品的生產.已知生產這種產品的成本價為每件30元,經過市場調研發現,該產品的銷售單價定在40到50元之間較為合理,并且該產品的年銷售量y(萬件)與銷售單價x(元)之間的關系如圖所示.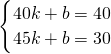 ,
, ,
,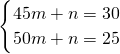 ,
,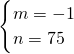 ,
, ;
; ,
,

科目:初中數學 來源: 題型:
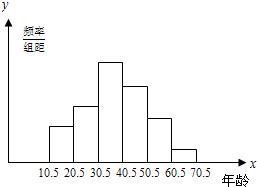 14、今年4月19日我市成功的舉辦了2005年菏澤國際牡丹花會,吸引了眾多的國內外貿易洽談及旅游觀光人士,起到了“以花為媒,促進菏澤經濟發展”的作用.花會期間,對六家大賓館、飯店中游客的年齡(年齡取整數)進行了抽樣統計,經整理后分成六組,并繪制成頻率分布直方圖,如圖所示.已知從左到右六個小組的頻率分別是0.08,0.20,0.32,0.24,0.12,0.04.第一小組頻數為8,請結合圖形回答下列問題:
14、今年4月19日我市成功的舉辦了2005年菏澤國際牡丹花會,吸引了眾多的國內外貿易洽談及旅游觀光人士,起到了“以花為媒,促進菏澤經濟發展”的作用.花會期間,對六家大賓館、飯店中游客的年齡(年齡取整數)進行了抽樣統計,經整理后分成六組,并繪制成頻率分布直方圖,如圖所示.已知從左到右六個小組的頻率分別是0.08,0.20,0.32,0.24,0.12,0.04.第一小組頻數為8,請結合圖形回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•海珠區一模)隨著經濟發展,污染問題日益嚴重.某環保廠家看到這個商機,以200萬元購買了某項空氣凈化產品的生產技術后,再投入280萬元購買生產設備進行該產品的生產.已知生產這種產品的成本價為每件30元,經過市場調研發現,該產品的銷售單價定在40到50元之間較為合理,并且該產品的年銷售量y(萬件)與銷售單價x(元)之間的關系如圖所示.
(2013•海珠區一模)隨著經濟發展,污染問題日益嚴重.某環保廠家看到這個商機,以200萬元購買了某項空氣凈化產品的生產技術后,再投入280萬元購買生產設備進行該產品的生產.已知生產這種產品的成本價為每件30元,經過市場調研發現,該產品的銷售單價定在40到50元之間較為合理,并且該產品的年銷售量y(萬件)與銷售單價x(元)之間的關系如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源:2013年廣東省廣州市海珠區中考數學一模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com