
【題目】如圖,在正方形ABCD中,邊長為2的等邊三角形AEF的頂點E、F分別在BC和CD上,下列結論:①CE=CF;②∠AEB=75°③BE+DF=EF;④CE= ![]() ,其中正確的結論的個數為( )
,其中正確的結論的個數為( )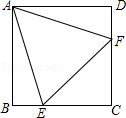
A.1個
B.2個
C.3個
D.4個
【答案】B
【解析】解:∵四邊形ABCD是正方形,
∴AB=AD,∠B=∠D=90°,
∵△AEF是等邊三角形,
∴AE=AF,
在Rt△ABE和Rt△ADF中,![]() ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=DC,
∴BC﹣BE=CD﹣DF,
∴CE=CF,故①正確;
∵CE=CF,
∴△ECF是等腰直角三角形,
∴∠CEF=45°,
∵∠AEF=60°,
∴∠AEB=75°,故②正確;
如圖,連接AC,交EF于G點,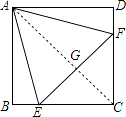
∴AC⊥EF,且AC平分EF,
∵∠FAD≠∠CAF,
∴DF≠FG,
∴BE+DF≠EF,故③錯誤;
∵EF=2,
∴CE=CF= ![]() ,故④錯誤.
,故④錯誤.
∴正確的有①②.
故選B.
【考點精析】根據題目的已知條件,利用等邊三角形的性質和正方形的性質的相關知識可以得到問題的答案,需要掌握等邊三角形的三個角都相等并且每個角都是60°;正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形.


科目:初中數學 來源: 題型:
【題目】)在信宜市某“三華李”種植基地有A,B兩個品種的樹苗出售,已知A種比B種每株多2元,買1株A種樹苗和2株B種樹苗共需20元.
(1)問A,B兩種樹苗每株分別是多少元?
(2)為擴大種植,某農戶準備購買A,B兩種樹苗共360株,且A種樹苗數量不少于B種數量的一半,請求出費用最省的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
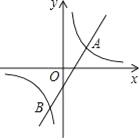
【題目】如圖,反比例函數![]() (k≠0)圖象經過點(1,2),并與直線y=2x+b交于點A(x1,y1),B(x2,y2),且滿足(x1+x2)(1﹣x1x2)=3.
(k≠0)圖象經過點(1,2),并與直線y=2x+b交于點A(x1,y1),B(x2,y2),且滿足(x1+x2)(1﹣x1x2)=3.
(1)求k的值;
(2)求b的值及點A,B的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
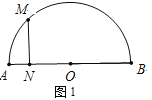
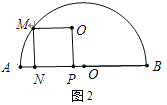
【題目】如圖1,半圓O的半徑![]() =5cm,點N是半徑AO上的一個動點(不與A、O重合),沿AO方向以1cm/s的速度向O點運動,過點N作MN⊥AB,交半圓O于點M,設運動時間為t s.
=5cm,點N是半徑AO上的一個動點(不與A、O重合),沿AO方向以1cm/s的速度向O點運動,過點N作MN⊥AB,交半圓O于點M,設運動時間為t s.
(1)求當t等于多少時,MN=3cm?
(2)如圖2,以MN為邊在半圓O內部作正方形MNPQ,使得點P落在AB上,點Q落在半圓內(或半圓上),設正方形MNPQ的面積為S.求S與t之間的函數關系式與自變量t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB是圓錐(如圖1)底面的直徑,P是圓錐的頂點,此圓錐的側面展開圖如圖2所示.一只螞蟻從A點出發,沿著圓錐側面經過PB上一點,最后回到A點.若此螞蟻所走的路線最短,那么M,N,S,T(M,N,S,T均在PB上)四個點中,它最有可能經過的點是( ) 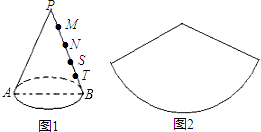
A.M
B.N
C.S
D.T
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三峽一期工程結束后的當年發電量為5.5×109度,某市有10萬戶居民,如果平均每戶每年用電2.75×103度,那么三峽工程該年所發的電能供該市居民使用多少年?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個點從數軸上的原點開始,先向右移動2個單位長度,再向左移動3個單位長度,經過兩次移動后到達的終點表示的是什么數?( )
A. +5 B. +1 C. -1 D. -5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把點(2,﹣3)先向右平移3個單位長度,再向上平移2個單位長度得到的點的坐標是( )
A.(5,﹣1)
B.(﹣1,﹣5)
C.(5,﹣5)
D.(﹣1,﹣1)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com