
【題目】已知直線![]() ,
,
(1)如圖1,點![]() 在直線
在直線![]() 上的左側,直接寫出
上的左側,直接寫出![]() ,
,![]() 和
和![]() 之間的數量關系是 .
之間的數量關系是 .
(2)如圖2,點![]() 在直線
在直線![]() 的左側,
的左側,![]() ,
,![]() 分別平分
分別平分![]() ,
,![]() ,直接寫出
,直接寫出![]() 和
和![]() 的數量關系是 .
的數量關系是 .
(3)如圖3,點![]() 在直線
在直線![]() 的右側
的右側![]() ,
,![]() 仍平分
仍平分![]() ,
,![]() ,那么
,那么![]() 和
和![]() 有怎樣的數量關系?請說明理由.
有怎樣的數量關系?請說明理由.

【答案】(1) ![]() ;(2)
;(2)![]() ;
;
(3)![]() .理由見解析
.理由見解析
【解析】
(1)首先作EF∥AB,根據直線AB∥CD,可得EF∥CD,所以∠ABE=∠1,∠CDE=∠2,據此推得∠ABE+∠CDE=∠BED即可.
(2)首先根據BF,DF分別平分∠ABE,∠CDE,推得∠ABF+∠CFD=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CFD,∠BED=∠ABE+∠CDE,據此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CFD,∠BED=∠ABE+∠CDE,據此推得∠BFD=![]() ∠BED.
∠BED.
(3)首先過點E作EG∥CD,再根據AB∥CD,EG∥CD,推得AB∥CD∥EG,所以∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,據此推得∠ABE+∠CDE+∠BED=360°;然后根據∠BFD=∠ABF+∠CDF,以及BF,DF分別平分∠ABE,∠CDE,推得2∠BFD+∠BED=360°即可.
解:(1)如圖1,作![]() ,
,
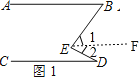 ,
,
![]() 直線
直線![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
即![]() .
.
(2)如圖2,
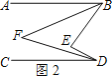 ,
,
![]() ,
,![]() 分別平分
分別平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]()
由(1),可得
![]()
![]() ,
,
![]() .
.
(3)如圖3,過點![]() 作
作![]() ,
,
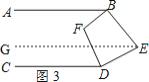 ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
由(1)知,![]() ,
,
又![]() ,
,![]() 分別平分
分別平分![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
故答案為:![]() 、
、![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上以
上以![]() 的速度由
的速度由![]() 點向
點向![]() 點運動(點
點運動(點![]() 不與點
不與點![]() 重合),同時點
重合),同時點![]() 在線段
在線段![]() 上由
上由![]() 點向
點向![]() 點運動.
點運動.

(1)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度相等,當運動時間是
的運動速度相等,當運動時間是![]() 時,
時,![]() 與
與![]() 是否全等?請說明理由;
是否全等?請說明理由;
(2)若點![]() 的運動速度與點
的運動速度與點![]() 的運動速度不相等,當
的運動速度不相等,當![]() 與
與![]() 全等時,點
全等時,點![]() 的運動時間是_______________;運動速度是_________________.
的運動時間是_______________;運動速度是_________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如下圖,![]() 和
和![]() 是等腰直接角三角形,
是等腰直接角三角形,![]() ,點
,點![]() 為
為![]() 邊上一點,連接
邊上一點,連接![]() ,
,![]() 交于點
交于點![]() ,點
,點![]() 恰好是
恰好是![]() 中點,連接
中點,連接![]() .
.
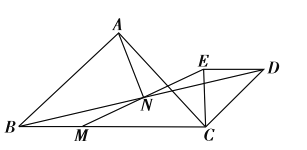
(1)求證:![]() ;
;
(2)連接AM、AE,請探究AN與EN的位置關系與數量關系。
①寫出AN與EM:位置關系___;數量關系___;
②請證明上述結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,![]() 為坐標原點,將三角形
為坐標原點,將三角形![]() 進行平移,平移后點
進行平移,平移后點![]() 的對應點分別是點
的對應點分別是點![]() ,點
,點![]() ,點
,點![]() ,點
,點![]() ,點
,點![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若點![]() ,其中
,其中![]() . 直線
. 直線![]() 交
交![]() 軸于點
軸于點![]() ,且三角形
,且三角形![]() 的面積為1,試探究
的面積為1,試探究![]() 和
和![]() 的數量關系,并說明理由.
的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義運算a![]() b=a(1-b),下面給出了關于這種運算的四個結論:
b=a(1-b),下面給出了關于這種運算的四個結論:
①2![]() (-2)=6 ②a
(-2)=6 ②a![]() b=b
b=b![]() a
a
③若a+b=0,則(a![]() a)+(b
a)+(b![]() b)=2ab ④若a
b)=2ab ④若a![]() b=0,則a=0.
b=0,則a=0.
其中正確結論的序號是 (填上你認為所有正確結論的序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,菱形![]() 的頂點
的頂點![]() 在
在![]() 軸上,點
軸上,點![]() 在點
在點![]() 的左側,點
的左側,點![]() 在
在![]() 軸的正半軸上.點
軸的正半軸上.點![]() 的坐標為
的坐標為![]() .動點
.動點![]() 從點
從點![]() 出發,以每秒1個單位長度的速度,按照
出發,以每秒1個單位長度的速度,按照![]() 的順序在菱形的邊上勻速運動一周,設運動時間為
的順序在菱形的邊上勻速運動一周,設運動時間為![]() 秒.
秒.
(1)①點![]() 的坐標 .②求菱形
的坐標 .②求菱形![]() 的面積.
的面積.
(2)當![]() 時,問線段
時,問線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 最小,如果存在,求出
最小,如果存在,求出![]() 最小值;如果不存在,請說明理由.
最小值;如果不存在,請說明理由.
(3)若點![]() 到
到![]() 的距離是1,則點
的距離是1,則點![]() 運動的時間
運動的時間![]() 等于 .
等于 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠1=∠2,要說明△ABD≌△ACD,還需從下列條件中選一個,錯誤的選法是( )
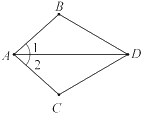
A. ∠ADB=∠ADCB. ∠B=∠CC. DB=DCD. AB=AC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一輛汽車往返于甲、乙兩地之間,如果汽車以50千米/時的平均速度從甲地出發,則6小時可到達乙地.
(1)寫出時間t(時)關于速度v(千米/時)的函數關系式,并畫出函數圖象.
(2)若這輛汽車需在5小時內從甲地到乙地,則此時汽車的平均速度至少應是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com