
【題目】數學老師布置了這樣一道作業題:
在△ABC中,AB=AC≠BC,點D和點A在直線BC的同側,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,連接AD,求∠ADB的度數.
小聰提供了研究這個問題的過程和思路:先從特殊問題開始研究,當α=90°,β=30°時(如圖1),利用軸對稱知識,以AB為對稱軸構造△ABD的軸對稱圖形△ABD′,連接CD′(如圖2),然后利用α=90°,β=30°以及等邊三角形的相關知識便可解決這個問題.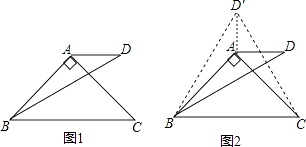
(1)請結合小聰研究問題的過程和思路,求出這種特殊情況下∠ADB的度數;
(2)結合小聰研究特殊問題的啟發,請解決數學老師布置的這道作業題;
(3)解決完老師布置的這道作業題后,小聰進一步思考,當點D和點A在直線BC的異側時,且∠ADB的度數與(1)中相同,則α,β滿足的條件為(直接寫出結果).
【答案】
(1)
解:如圖1

作∠AB D′=∠ABD,B D′=BD,連接CD′,AD′,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵∠DBC=30°,
∴∠ABD=∠ABC﹣∠DBC=15°,
∵AB=AB,∠AB D′=∠ABD,B D′=BD,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等邊三角形,
∴D′B=D′C,∠BD′C=60°,
∵AB=AC,AD'=AD',
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B= ![]() ∠BD′C=30°,
∠BD′C=30°,
∴∠ADB=30°
(2)
解:第一種情況:當60°<α≤120°時,

如圖2,作∠AB D′=∠ABD,B D′=BD,連接CD′,AD′,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC= ![]() =90°﹣
=90°﹣ ![]() ,
,
∴∠ABD=∠ABC﹣∠DBC=90°﹣ ![]() ﹣β,
﹣β,
同(1)可證△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°﹣ ![]() ﹣β,BD=BD′,∠ADB=∠AD′B
﹣β,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°﹣ ![]() =180°﹣(α+β),
=180°﹣(α+β),
∵α+β=120°,
∴∠D′BC=60°,
以下同(1)可求得∠ADB=30°,
第二種情況:當0°<α<60°時,
如圖3,

作∠AB D′=∠ABD,B D′=BD,連接CD′,AD′.同理可得:∠ABC= ![]() ,
,
∴∠ABD=∠DBC﹣∠ABC= ![]() ,
,
同(1)可證△ABD≌△ABD′,
∴∠ABD=∠ABD′= ![]() ,BD=BD′,∠ADB=∠AD′B,
,BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC﹣∠ABD′=90°﹣ ![]() ,
,
∴D′B=D′C,∠BD′C=60°.
同(1)可證△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°
(3)0°<α<120°,β=60°或120°<α<180°,0<β<60°時,α﹣β=120°或120°<α<180°,β=60°
【解析】解:(3)點D和點A在直線BC的異側時,分三種情況討論:
第一種情況:如圖4,
當120°<α<180°,β=60°時,連接CD,
∵∠DBC=β=60°,BD=BC,
∴△DBC是等邊三角形,
∴BD=CD,
∴△ABD≌△ACD,
∴∠ADB=∠ADC=30°,
第二種情況:如圖5,
當120°<α<180°,0<β<60°時,連接CD′,
∠ABC= ![]() =90°﹣
=90°﹣ ![]() ,
,
∠ABD=∠ABC+∠DBC=90°﹣ ![]() +β,
+β,
∵△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°﹣ ![]() +β,
+β,
∵∠ADB=∠AD′B=30°,
∴∠BD′C=60°,
∵BD′=CD′,
∴△BD′C是等邊三角形,
∴∠CBD′=(90°﹣ ![]() +β)+(90°﹣
+β)+(90°﹣ ![]() )=60°,
)=60°,
∴α﹣β=120°,
第三種情況:如圖6,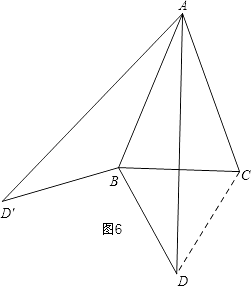
當0°<α<120°,β=60°時,連接CD,
與圖4同理得:∠ADB=∠ADC=30°,
所以答案是:0°<α<120°,β=60°或120°<α<180°,0<β<60°時,α﹣β=120°或120°<α<180°,β=60°.
【考點精析】關于本題考查的全等三角形的性質,需要了解全等三角形的對應邊相等; 全等三角形的對應角相等才能得出正確答案.


 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】如圖1,我們在2016年1月的日歷中標出一個十字星,并計算它的“十字差”(將十字星左右兩數,上下兩數分別相乘再將所得的積作差,稱為該十字星的“十字差”).該十字星的十字差為12×14﹣6×20=48,再選擇其它位置的十字星,可以發現“十字差”仍為48. 
(1)如圖2,將正整數依次填入5列的長方形數表中,探究不同位置十字星的“十字差”,可以發現相應的“十字差”也是一個定值,則這個定值為 . 
(2)若將正整數依次填入k列的長方形數表中(k≥3),繼續前面的探究,可以發現相應“十字差”為與列數k有關的定值,請用k表示出這個定值,并證明你的結論.
(3)如圖3,將正整數依次填入三角形的數表中,探究不同十字星的“十字差”,若某個十字星中心的數在第32行,且其相應的“十字差”為2015,則這個十字星中心的數為(直接寫出結果). 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,正方形ABCD的位置如圖所示,點A的坐標為(1,0),點D的坐標為(0,2).延長CB交x軸于點A1,作第1個正方形A1B1C1C;延長C1B1交x軸于點A2,作第2個正方形A2B2C2C1,…,按這樣的規律進行下去,第2016個正方形的面積是 .
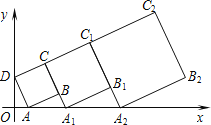
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com