
【題目】在平面直角坐標系中,正方形![]() 的點
的點![]() ,
,![]() ,
,![]() ,現將此正方形繞
,現將此正方形繞![]() 逆時針旋轉
逆時針旋轉![]() ,得到正方形
,得到正方形![]() ,求正方形
,求正方形![]() 各頂點的坐標.
各頂點的坐標.
【答案】![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
作A1D⊥x軸于D,C1E⊥x軸于E,如圖,根據正方形的性質得OB=2![]() ,∠BOA=∠BOC=45°,再根據旋轉的性質得點B1在y軸上,OB1=OB=2
,∠BOA=∠BOC=45°,再根據旋轉的性質得點B1在y軸上,OB1=OB=2![]() ,∠A1OD=45°,∠B1OC1=45°,OA1=OA=OC1=2,則可判斷△A1OD和△EOC1都是等腰直角三角形,于是可根據等腰直角三角形的性質得到A1D=OD=
,∠A1OD=45°,∠B1OC1=45°,OA1=OA=OC1=2,則可判斷△A1OD和△EOC1都是等腰直角三角形,于是可根據等腰直角三角形的性質得到A1D=OD=![]() OA1=
OA1=![]() ,C1E=OE=
,C1E=OE=![]() OC1=
OC1=![]() ,然后根據各象限點的坐標特征和y軸上點的坐標特征寫出正方形OA1B1C1各頂點的坐標.
,然后根據各象限點的坐標特征和y軸上點的坐標特征寫出正方形OA1B1C1各頂點的坐標.
解:作![]() 軸于
軸于![]() ,
,![]() 軸于
軸于![]() ,如圖,
,如圖,
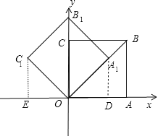
∵正方形![]() 的點
的點![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴正方形![]() 繞
繞![]() 逆時針旋轉
逆時針旋轉![]() ,得到正方形
,得到正方形![]() ,
,
∴點![]() 在
在![]() 軸上,
軸上,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() .
.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:初中數學 來源: 題型:
【題目】(題文)(題文)等邊![]() 在平面直角坐標系中,已知點
在平面直角坐標系中,已知點![]() ,將
,將![]() 繞點O順時針方向旋轉
繞點O順時針方向旋轉![]() 得
得![]() .
.
![]() 求出點B的坐標;
求出點B的坐標;
![]() 當
當![]() 與
與![]() 的縱坐標相同時,求出a的值;
的縱坐標相同時,求出a的值;
![]() 在
在![]() 的條件下直接寫出點
的條件下直接寫出點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足為D,AF平分∠CAB,交CD于點E,交CB于點F.若AC=6,AB=10,則DE的長為______

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在關于x的分式方程![]() ①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均為實數,方程①的根為非負數.
①和一元二次方程(2﹣k)x2+3mx+(3﹣k)n=0②中,k、m、n均為實數,方程①的根為非負數.
(1)求k的取值范圍;
(2)當方程②有兩個整數根x1、x2,k為整數,且k=m+2,n=1時,求方程②的整數根;
(3)當方程②有兩個實數根x1、x2,滿足x1(x1﹣k)+x2(x2﹣k)=(x1﹣k)(x2﹣k),且k為負整數時,試判斷|m|≤2是否成立?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=BC=AC=12cm,現有兩點M、N分別從點A. 點B同時出發,沿三角形的邊運動,已知點M的速度為1cm/s,點N的速度為2cm/s.當點N第一次到達B點時,M、N同時停止運動.
(1)點M、N運動_________秒后,△AMN是等邊三角形?
(2)點M、N在BC邊上運動時,運動_______秒后得到以MN為底邊的等腰三角形△AMN?
(3)M、N同時運動幾秒后,△AMN是直角三角形?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,AC=BC=4cm,點D是斜邊AB的中點,點E從點B出發以1cm/s的速度向點C運動,點F同時從點C出發以一定的速度沿射線CA方向運動,規定:當點E到終點C時停止運動;設運動的時間為x秒,連接DE、DF.
(1)填空:S△ABC= cm2;
(2)當x=1且點F運動的速度也是1cm/s時,求證:DE=DF;
(3)若動點F以3cm/s的速度沿射線CA方向運動;在點E、點F運動過程中,如果有某個時間x,使得△ADF的面積與△BDE的面積存在兩倍關系,請你直接寫出時間x的值;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】自![]() 年
年![]() 月
月![]() 日零時起,高鐵開通,某旅行社為吸引廣大市民組團去仙都旅游,推出了如下收費標準:如果人數不超過
日零時起,高鐵開通,某旅行社為吸引廣大市民組團去仙都旅游,推出了如下收費標準:如果人數不超過![]() 人,人均旅游費用為
人,人均旅游費用為![]() 元,如果人數超過
元,如果人數超過![]() 人,每增加
人,每增加![]() 人,人均旅游費用降低
人,人均旅游費用降低![]() 元,但人均旅游費用不得低于
元,但人均旅游費用不得低于![]() 元.
元.
![]() 如果某單位組織
如果某單位組織![]() 人參加仙都旅游,那么需支付旅行社旅游費用________元;
人參加仙都旅游,那么需支付旅行社旅游費用________元;
![]() 現某單位組織員工去仙都旅游,共支付給該旅行社旅游費用
現某單位組織員工去仙都旅游,共支付給該旅行社旅游費用![]() 元,那么該單位有多少名員工參加旅游?
元,那么該單位有多少名員工參加旅游?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com