
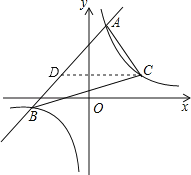
【題目】已知一次函數y1=x+m的圖象與反比例函數![]() 的圖象交于A、B兩點.已知當x>1時,y1>y2;當0<x<1時,y1<y2.
的圖象交于A、B兩點.已知當x>1時,y1>y2;當0<x<1時,y1<y2.

(1)求一次函數的解析式;
(2)已知雙曲線在第一象限上有一點C到y軸的距離為3,求△ABC的面積.
【答案】(1)y1=x+5 (2)21
【解析】
試題分析:(1)首先根據x>1時,y1>y2,0<x<1時,y1<y2確定點A的橫坐標,然后代入反比例函數解析式求出點A的縱坐標,從而得到點A的坐標,再利用待定系數法求直線解析式解答;
(2)根據點C到y軸的距離判斷出點C的橫坐標,代入反比例函數解析式求出縱坐標,從而得到點C的坐標,過點C作CD∥x軸交直線AB于D,求出點D的坐標,然后得到CD的長度,再聯立一次函數與雙曲線解析式求出點B的坐標,然后△ABC的面積=△ACD的面積+△BCD的面積,列式進行計算即可得解.
解:(1)∵當x>1時,y1>y2;當0<x<1時,y1<y2,
∴點A的橫坐標為1,
代入反比例函數解析式,![]() =y,
=y,
解得y=6,
∴點A的坐標為(1,6),
又∵點A在一次函數圖象上,
∴1+m=6,
解得m=5,
∴一次函數的解析式為y1=x+5;
(2)∵第一象限內點C到y軸的距離為3,
∴點C的橫坐標為3,
∴y=![]() =2,
=2,
∴點C的坐標為(3,2),
過點C作CD∥x軸交直線AB于D,
則點D的縱坐標為2,
∴x+5=2,
解得x=﹣3,
∴點D的坐標為(﹣3,2),
∴CD=3﹣(﹣3)=3+3=6,
點A到CD的距離為6﹣2=4,
聯立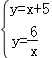 ,
,
解得![]() (舍去),
(舍去),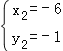 ,
,
∴點B的坐標為(﹣6,﹣1),
∴點B到CD的距離為2﹣(﹣1)=2+1=3,
S△ABC=S△ACD+S△BCD=![]() ×6×4+
×6×4+![]() ×6×3=12+9=21.
×6×3=12+9=21.


科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCO中,點C在x軸上,點A在y軸上,點B的坐標是(一6,8).矩形ABCO沿直線BD折疊,使得點A落在對角線OB上的點E處,折痕與OA、x軸分別交于點D、F.

(1)直接寫出線段BO的長:
(2)求點D的坐標;
(3)若點N是平面內任一點,在x軸上是否存在點M,使咀M、N、E、O為頂點的四邊形是菱形?若存在,請直接寫出滿足條件的點M的坐標:若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在物理實驗中,當電流在一定時間段內正常通過電子元件時,每個電子元件的狀態有兩種可能:通電或斷開,并且這兩種狀態的可能性相等.
(1)如圖1,當有2個電子元件![]() 并聯時,請你用樹狀圖表示圖中
并聯時,請你用樹狀圖表示圖中![]() 之間電流能否通過的所有可能情況,并求出
之間電流能否通過的所有可能情況,并求出![]() 之間電流通過的概率;
之間電流通過的概率;
(2)如圖2,當有3個電子元件并聯時,求![]() 之間電流通過的概率.
之間電流通過的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某自行車廠一周計劃生產![]() 輛自行車,平均每天生產
輛自行車,平均每天生產![]() 輛,由于各種原因實際每天生產量與計劃量相比有出入,下表是某周的生產情況(超產為正,減產為負);
輛,由于各種原因實際每天生產量與計劃量相比有出入,下表是某周的生產情況(超產為正,減產為負);
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增減 |
|
|
|
|
|
|
|
![]() 根據記錄可知前三天共生產________輛;
根據記錄可知前三天共生產________輛;
![]() 產量最多的一天比產量最少的一天多生產________輛;
產量最多的一天比產量最少的一天多生產________輛;
![]() 該廠實行計件工資制,每輛車
該廠實行計件工資制,每輛車![]() 元,超額完成任務每輛獎
元,超額完成任務每輛獎![]() 元,少生產一輛扣
元,少生產一輛扣![]() 元,那么該廠工人這一周的工資總額是多少?
元,那么該廠工人這一周的工資總額是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在![]() 中,分別以
中,分別以![]() 、
、![]() 為斜邊,向
為斜邊,向![]() 的形外作等腰直角三角形,直角的頂點分別為
的形外作等腰直角三角形,直角的頂點分別為![]() ,點
,點![]() 分別為
分別為![]() 邊的中點.問:
邊的中點.問: ![]() 是否全等?____(填“是”或“否”);
是否全等?____(填“是”或“否”);
(2)如圖2,在![]() 中,分別以
中,分別以![]() 為底邊,向
為底邊,向![]() 的形外作等腰三角形,頂角的頂點分別為
的形外作等腰三角形,頂角的頂點分別為![]() ,且
,且![]() .點
.點![]() 分別為
分別為![]()
![]() 邊的中點.
邊的中點.
①試判斷![]() 是否滿足(1)中的關系?若滿足,請說明理由;若不滿足,請寫
是否滿足(1)中的關系?若滿足,請說明理由;若不滿足,請寫![]() 之間存在的一種關系,并加以說明.
之間存在的一種關系,并加以說明.
②若![]() ,
, ![]() ,
, ![]() 的面積為32,求
的面積為32,求![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級640名學生在“計算機應用”培訓前、后各參加了一次水平相同的測試,并以同一標準分成“不合格”、“合格”、“優秀”3個等級,為了解培訓效果,用抽樣調查的方式從中抽取32名學生的2次測試等級,并繪制成條形統計圖:

(1)這32名學生經過培訓,測試等級“不合格”的百分比比培訓前減少了多少?
(2)估計該校八年級學生中,培訓前、后等級為“合格”與“優秀”的學生各有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面的圖像反映的過程是:小明從家去超市買文具,又去書店購書,然后回家.其中x表示時間,y表示小明離他家的距離,若小明家、超市、書店在同一條直線上.
根據圖像回答下列問題:

(1)超市離小明家多遠,小明走到超市用了多少時間?
(2)超市離書店多遠,小明在書店購書用了多少時間?
(3)書店離小明家多遠,小明從書店走回家的平均速度是每分鐘多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,△ABC內接于⊙O,AC是直徑,點D是AC延長線上一點,且∠DBC=∠BAC, ![]() .
.
(1) 求證:BD是⊙O的切線;
(2) 求![]() 的值;
的值;
(3) 如圖2,過點B作BG⊥AC交AC于點F,交⊙O于點G,BC、AG的延長線交于點E,⊙O的半徑為6,求BE的長.
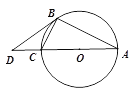
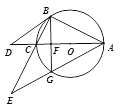
圖1 圖2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】節約用水是我們的美德,水龍頭關閉不嚴會造成滴水,容器內盛水![]() 與滴水時間
與滴水時間![]() 的關系用可以顯示水量的容器做如圖
的關系用可以顯示水量的容器做如圖![]() 的試驗,并根據試驗數據繪制出如圖
的試驗,并根據試驗數據繪制出如圖![]() 的函數圖象,結合圖象解答下列問題.
的函數圖象,結合圖象解答下列問題.
(![]() )容器內原有水多少升.
)容器內原有水多少升.
(![]() )求
)求![]() 與
與![]() 之間的函數關系式,并計算在這種滴水狀態下一天的滴水量是多少升.
之間的函數關系式,并計算在這種滴水狀態下一天的滴水量是多少升.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com