
【題目】如圖,有理數 a,b,c 分別對應數軸上的點 A,B,C,若a 2![]() |b 4| 0 ,關于 x、y 的單項式3(c 3)x
|b 4| 0 ,關于 x、y 的單項式3(c 3)x![]() y
y![]() 與 y
與 y![]() x 是同類項. 我們把數軸上兩點之間的距離用表示兩點的大寫字母一起標記,例如,點 A 與點 B 間的距離記作 AB.
x 是同類項. 我們把數軸上兩點之間的距離用表示兩點的大寫字母一起標記,例如,點 A 與點 B 間的距離記作 AB.
![]()
![]()
(1)求 a,b,c 的值;
(2)點 P 從 C 點出發以每秒 1 個單位長度在數軸上按以下規律往返運動:第一回合,從點 C 到點 B 到點 A 回到點 C;第二回合,從點 C 到 BC 的中點 D 到 CA 的中點 D1 回到點 C;第三回合,從點 C 到 CD 的中點 D2 到 CD1 的中點 D3 回到點 C……,如此循環下去,若第 t 秒時滿足 PB+2PC=AC+1,求 t 的最大值;
(3)在(2)的條件下,P 點第一次從 C 點出發的同時,數軸上的動點 M、N 分別從 A 點和 B 點向右運動,速度分別為每秒 1 個單位長度和每秒 2 個單位長度,P 點完成第一個回合后停止在 C 點,當 MP=2MN 時, t 的值是 (直接填答案)
【答案】(1)a=2,b=-4,c=-1;(2)最大值為![]() 秒;(3)
秒;(3)![]() 秒.
秒.
【解析】
(1)根據絕對值和偶次冪的非負性可以求出a、b,再根據同類項的定義求c即可.
(2)首先根據第一回合計算出滿足PB+2PC=AC+1時的t值,從而得到要滿足PB+2PC=AC+1的點P所對應的數,進而分析第幾回合到達不了這個數,從而求最大值;
(3)分析N追上M時t的值,據此進行分類討論.
(1)∵![]() ,3(c 3)x
,3(c 3)x![]() y
y![]() 與 y
與 y![]() x 是同類項
x 是同類項
∴a-2=0,b+4=0,|c+2|=1且c+3≠0,
∴a=2,b=-4,c=-1.
(2)由(1)知,點A對應的數為2,點B對應的數為-4,點C對應的數為-1,則AC=3,
第一回合:當點P從C到B時,CP=t,BP=3-t,
∵PB+2PC=AC+1
∴3-t+2t=4,則t=1,此時點P對應的數為-2,
當點P從C到A時,CP=t-6,BP=3+t-6=t-3,
∵PB+2PC=AC+1
∴t-3+2(t-6)=4,則t=![]() ,此時點P對應的數為
,此時點P對應的數為![]() ,
,
通過計算可得,D4對應的數為![]() ,D5對應的數為
,D5對應的數為![]() ,D6對應的數為
,D6對應的數為![]() >-2,D7對應的數為
>-2,D7對應的數為![]() <
<![]() ,所以t的最大值在第三回合點P從D5回到點C時取得.
,所以t的最大值在第三回合點P從D5回到點C時取得.
此時CP= ![]() ,BP=
,BP= ![]() ,
,
∴![]() ,則
,則![]() ,
,
故滿足PB+2PC=AC+1時,t的最大值為![]() 秒.
秒.
(3)由題可得,AC==BC=3,點P運動路程為t,點M運動路程為t,點N運動路程為2t,
令2t-t=6,解得t=6,則運動6秒后N追上M,
①追上前(![]() ):MN=6+t-2t=6-t,
):MN=6+t-2t=6-t,
當![]() 時,MP=t+3+t=2t+3,則2t+3=2(6-t),解得
時,MP=t+3+t=2t+3,則2t+3=2(6-t),解得![]() ,
,
當![]() 時,MP= t+3+(6-t)=9,則9=2(6-t),解得
時,MP= t+3+(6-t)=9,則9=2(6-t),解得![]() ,不滿足條件舍去;
,不滿足條件舍去;
②追上后(![]() ):MN=2t-6-t =t-6,
):MN=2t-6-t =t-6,
當![]() 時,MP=9-t+t=9,則9=2(t-6),解得
時,MP=9-t+t=9,則9=2(t-6),解得![]() ,不滿足條件舍去,
,不滿足條件舍去,
當![]() 時,MP= t-9+t=2t-9,則2t-9=2(t-6),無解;
時,MP= t-9+t=2t-9,則2t-9=2(t-6),無解;
綜上所述,t值為![]() 秒.
秒.


科目:初中數學 來源: 題型:
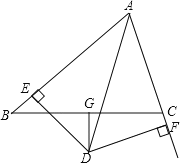
【題目】如圖,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)判斷BE與CF的數量關系,并說明理由;
(2)如果AB=8,AC=6,求AE、BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若規定這樣一種運算:a△b=![]() (|ab|+a+b),例如:2△3=
(|ab|+a+b),例如:2△3=![]() (|23|+2+3)=3
(|23|+2+3)=3
(1)求3△4和(-3)△(-2)的值;
(2)將1,2,3,…,50這50個自然數,任意分為25組,每組兩個數,現將每組的兩個數中任一數值記作a,另一個記作b,代入代數式![]() (|ab|+a+b)中進行計算,求出其結果,25組數代入后可求得25個值,求這25個值的和的最大值是_____.
(|ab|+a+b)中進行計算,求出其結果,25組數代入后可求得25個值,求這25個值的和的最大值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
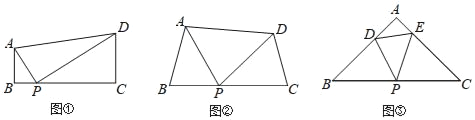
【題目】如圖①,在四邊形ABCD中,AB∥CD,∠B=90°,點P在BC邊上,當∠APD=90° 時,可知△ABP∽△PCD.(不要求證明)
(1)探究:如圖②,在四邊形ABCD中,點P在BC邊上,當∠B=∠C=∠APD時,求證:△ABP∽△PCD.
(2)拓展:如圖③,在△ABC中,點P是邊BC的中點,點D、E分別在邊AB、AC上若∠B=∠C=∠DPE=45°,BC=8![]() ,CE=6,則DE的長為 .
,CE=6,則DE的長為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】公園的門票價格規定如下表:
購票張數 | 1 到 50 張 | 51 到 100 張 | 101 到 150張 | 150 張以上 |
每張票的價格 | 12 元 | 10 元 | 8 元 | 超過 150 張的部分 7 元 |
某校七年級(1)(2)兩個班共 104 人,其中(1)班 40 多人,不足 50 人,經估算,如果兩個班都以班為單位購票,則一共應付 1136 元,問:
(1)若兩班聯合起來作為一個團體購票,可省多少錢?
(2)兩班學生各有多少人?
(3)若七年級(3)班有 n 人(46<n<55)與(1),(2)班一起去游園,某商家贊助,支付三個班的所有門票費,則該商家最少花費 元(用含 n 的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在△ABC中,BE、CF分別是AC、AB兩邊上的高,在BE上截取BD=AC,在CF的延長線上截取CG=AB,連接AD、AG.
(1)求證:AD=AG;
(2)AD與AG的位置關系如何,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD的邊AB在x軸上,點C的坐標為(﹣5,4),點D在y軸的正半軸上,經過點A的直線y=![]() x﹣1與y軸交于點E,將直線AE沿y軸向上平移n(n>0)個單位長度后,得到直線l,直線l經過點C時停止平移.
x﹣1與y軸交于點E,將直線AE沿y軸向上平移n(n>0)個單位長度后,得到直線l,直線l經過點C時停止平移.
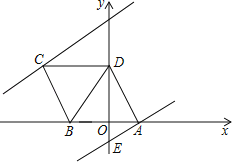
(1)點A的坐標為 ,點B的坐標為 ;
(2)若直線l交y軸于點F,連接CF,設△CDF的面積為S(這里規定:線段是面積為0的三角形),求S與n之間的函數關系式,并寫出n的取值范圍;
(3)易知AE⊥AD于點A,若直線l交折線AD﹣DC于點P,當△AEP為直角三角形時,請直接寫出n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1、2,已知四邊形ABCD為正方形,在射線AC上有一動點P,作PE⊥AD(或延長線)于E,作PF⊥DC(或延長線)于F,作射線BP交EF于G.
(1)在圖1中,設正方形ABCD的邊長為2,四邊形ABFE的面積為y,AP=x,求y關于x的函數表達式;
(2)結論:GB⊥EF對圖1,圖2都是成立的,請任選一圖形給出證明;
(3)請根據圖2證明:△FGC∽△PFB.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把邊長為2的等邊三角形△ABC沿直線BC向右平移,使點B與點C重合,得到△DCE,連接BD,交AC于點F.
(1)證明:AC⊥BD;
(2)求線段BD的長。

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com