
【題目】如圖,在四邊形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
, ![]() ,動點P從點D出發,沿線段
,動點P從點D出發,沿線段 ![]() 的方向以每秒2個單位長的速度運動;動點Q從點 C出發,在線段
的方向以每秒2個單位長的速度運動;動點Q從點 C出發,在線段 ![]() 上以每秒1個單位長的速度向點
上以每秒1個單位長的速度向點![]() 運動;點P,
運動;點P,![]() 分別從點D,C同時出發,當點
分別從點D,C同時出發,當點![]() 運動到點
運動到點 ![]() 時,點Q隨之停止運動,設運動的時間為t秒).
時,點Q隨之停止運動,設運動的時間為t秒).

(1)當 ![]() 時,求
時,求 ![]() 的面積;
的面積;
(2)若四邊形![]() 為平行四邊形,求運動時間
為平行四邊形,求運動時間![]() .
.
(3)當 ![]() 為何值時,以 B、P、Q為頂點的三角形是等腰三角形?
為何值時,以 B、P、Q為頂點的三角形是等腰三角形?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)過點![]() 作
作![]() 于
于![]() ,則PM=DC,當t=2時,算出BQ,求出面積即可;(2)當四邊形
,則PM=DC,當t=2時,算出BQ,求出面積即可;(2)當四邊形![]() 是平行四邊形時,
是平行四邊形時,![]() ,即
,即![]() ,解出即可;(3)以 B、P、Q為頂點的三角形是等腰三角形,分三種情況,①
,解出即可;(3)以 B、P、Q為頂點的三角形是等腰三角形,分三種情況,①![]() ,②
,②![]() ,③
,③![]() 分別求出t即可.
分別求出t即可.
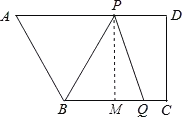
解 :(1)過點![]() 作
作![]() 于
于![]() ,則四邊形
,則四邊形![]() 為矩形.
為矩形.
∴![]() ,
,
∵![]() ,
,
當t=2時,則BQ=14,
則![]() =
=![]() ×14×12=84;
×14×12=84;
(2)當四邊形![]() 是平行四邊形時,
是平行四邊形時,![]() ,
,
即![]()
解得:![]()
∴當![]() 時,四邊形
時,四邊形![]() 是平行四邊形.
是平行四邊形.
(3)由圖可知,CM=PD=2t,CQ=t,若以B、P、Q為頂點的三角形是等腰三角形,可以分為以下三種情況:
①若![]() ,在
,在![]() 中,
中,![]() ,由
,由![]() 得
得![]() 解得:
解得:![]() ;
;
②若![]() ,在
,在![]() 中,
中,![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,
,
此時,![]() ,
,
所以此方程無解,所以![]() ;
;
③若![]() ,由
,由![]() 得
得![]() ,
,
得 ![]() ,
,![]() (不合題意,舍去);
(不合題意,舍去);
綜上所述,當![]() 或
或![]() 時,以B、P、Q為頂點的三角形是等腰三角形.
時,以B、P、Q為頂點的三角形是等腰三角形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,從左邊第一個格子開始向右數,在每個小格子中都填入一個整數,使得其中任意三個相鄰格子中所填整數之和都相等.
|
|
|
|
|
| ··· |
![]() 可求得
可求得![]() ,第
,第![]() 個格子中的數為 ;
個格子中的數為 ;
![]() 判斷:前
判斷:前![]() 個格子中所填整數之和是否可能為
個格子中所填整數之和是否可能為![]() 若能,求出
若能,求出![]() 的值,若不可能,請說明理由;
的值,若不可能,請說明理由;
![]() 如果
如果![]() ,
,![]() 為前
為前![]() 格子中的任意兩個數,那么所有
格子中的任意兩個數,那么所有![]() 的和可以通過計算
的和可以通過計算
![]() 得到,若
得到,若![]() span>,
span>,![]() 為前
為前![]() 格子中的任意兩個數,則所有
格子中的任意兩個數,則所有![]() 的的和為
的的和為
查看答案和解析>>
科目:初中數學 來源: 題型:
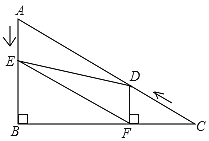
【題目】如圖,在Rt△ABC中,∠B=90°,AC=10,∠C=30°,點D從點C出發沿CA方向以每秒2個單位長度的速度向點A勻速運動,同時點E從點A出發沿AB方向以每秒1個單位長度的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是t(t>0)秒,過點D作DF⊥BC于點F,連接DE、EF.
(1)求證:四邊形AEFD是平行四邊形;
(2)當t為何值時,△DEF是等邊三角形?說明理由;
(3)當t為何值時,△DEF為直角三角形?(請直接寫出t的值)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A、B、C、D均在⊙O上,FB與⊙O相切于點B,AB與CF交于點G,OA⊥CF于點E,AC∥BF.
(1)求證:FG=FB.
(2)若tan∠F=![]() ,⊙O的半徑為4,求CD的長.
,⊙O的半徑為4,求CD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
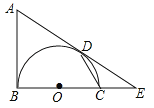
【題目】(2016浙江省麗水市)如圖,AB是以BC為直徑的半圓O的切線,D為半圓上一點,AD=AB,AD,BC的延長線相交于點E.
(1)求證:AD是半圓O的切線;
(2)連結CD,求證:∠A=2∠CDE;
(3)若∠CDE=27°,OB=2,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,要建一個面積為150 m2的矩形養雞場,為了節約材料,養雞場的一邊沿用原來的一堵墻,墻長為a m,其余三邊用竹籬笆圍成,已知竹籬笆的長為35 m.
(1)如果a=40,那么養雞場的長和寬各為多少米?
(2)如果a是一個可以變化的量,那么墻的長度a對所建的養雞場有怎樣的影響?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)由大小相同的小立方塊搭成的幾何體如圖1,請在圖2的方格中畫出該幾何體的俯視圖和左視圖.
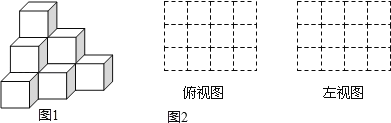
(2)用小立方體搭一個幾何體,使得它的俯視圖和左視圖與你在方格中所畫的一致,則這樣的幾何體最少要 個小立方塊,最多要 個小立方塊.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在平面直角坐標系中,點A的坐標為(m,0),點B的坐標為(0,n),其中m=![]() ,
,![]() =0,將三角形BOA沿x軸的正方向向右平移10個單位長度得到三角形CDE,連接BC.
=0,將三角形BOA沿x軸的正方向向右平移10個單位長度得到三角形CDE,連接BC.
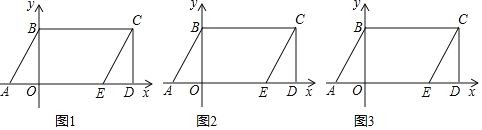
(1)如圖1,分別求點C、點E的坐標;
(2)點P自點C出發,以每秒1個單位長度沿線段CB運動,同時點Q自點O出發,以每秒2個單位長度沿線段OE運動,連接AP、BQ,點Q運動至點E時,點P同時停止運動.設運動時間t(秒),三角形ABQ的面積與三角形APB的面積的和為s(平方單位),求s與t的關系式,并直接寫出t的取值范圍;
(3)在(2)的條件下,BP:QE=8:3,此時將線段PQ向左平移2個單位長度得到線段P'Q'(點P'與點P對應),線段P′Q'再向下平移2個單位長度得到線段MN(點M與點P'對應),線段MN交x軸于點G,點H在線段OA上,OH=![]() OG,過點H作HR⊥OA,交AB于點R,求點R的坐標.
OG,過點H作HR⊥OA,交AB于點R,求點R的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com