
【題目】近年來,新能源汽車以其舒適環保、節能經濟的優勢受到熱捧,隨之而來的就是新能汽車銷量的急速增加,當前市場上新能漂汽車從動力上分純電動和混合動力兩種,從用途上又分為乘用式和商用式兩種,據中國汽車工業協會提供的信息,2017年全年新能源乘用車的累計銷量為57.9萬輛,其中,純電動乘用車銷量為46.8萬輛,混合動力乘用車銷量為11.1萬輛; 2017年全年新能源商用車的累計銷量為19.8萬輛,其中,純電動商用車銷量為18.4萬輛,混合動力商用車銷量為1.4萬輛,請根據以上材料解答下列問題:
(1)請用統計表表示我國2017年新能源汽車各類車型銷量情況;
(2)小穎根據上述信息,計算出2017年我國新能源各類車型總銷量為77.7萬輛,并繪制了“2017年我國新能源汽車四類車型銷量比例”的扇形統計圖,如圖1,請你將該圖補充完整(其中的百分數精確到0.1%);
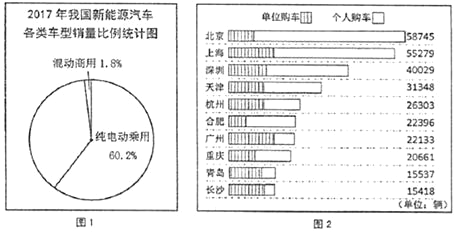
(3)2017年我國新能源乘用車銷量最高的十個城市排名情況如圖2,請根據圖2中信息寫出這些城市新能源乘用車銷售情況的特點(寫出一條即可);
(4)數據顯示,2018年1~3月的新能源乘用車總銷量排行榜上位居前四的廠家是比亞迪、北汽、上汽、江準,參加社會實踐的大學生小王想對其中兩個廠家進行深入調研,他將四個完全相同的乒乓球進行編號(用“1,2,3,4”依次對應上述四個廠家),并將乒乓球放入不透明的袋子中攪勻,從中一次拿出兩個乒乓球,根據乒乓球上的編號決定要調研的廠家.求小王恰好調研“比亞迪”和“江淮”這兩個廠家的概率.
【答案】(1)統計表見解析;(2)補全圖形見解析;(3)總銷量越高,其個人購買量越大;
(4)![]() .
.
【解析】
(1)認真讀題,找到題目中的相關信息量,列表統計即可;
(2)分別求出“混動乘用”和“純電動商用”的圓心角的度數,然后補扇形圖即可;
(3)根據圖表信息寫出一個符合條件的信息即可;
(4)利用樹狀圖確定求解概率.
(1)統計表如下:
2017年新能源汽車各類型車型銷量情況(單位:萬輛) | |||
類型 | 純電動 | 混合動力 | 總計 |
新能源乘用車 | 46.8 | 11.1 | 57.9 |
新能源商用車 | 18.4 | 1.4 | 19.8 |
(2)混動乘用:![]() ×100%≈14.3%,14.3%×360°≈51.5°,
×100%≈14.3%,14.3%×360°≈51.5°,
純電動商用:![]() ×100%≈23.7%,23.7%×360°≈85.3°,
×100%≈23.7%,23.7%×360°≈85.3°,
補全圖形如下:
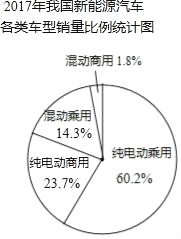
(3)總銷量越高,其個人購買量越大.
(4)畫樹狀圖如下:
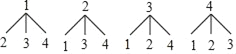
∵一共有12種等可能的情況數,其中抽中1、4的情況有2種,
∴小王恰好調研“比亞迪”和“江淮”這兩個廠家的概率為![]() =
=![]() .
.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
【題目】△ABC是等邊三角形,P為平面內的一個動點,BP=BA,0<∠PBC<180 ,DB平分∠PBC,且DB=DA.

(1)當BP與BA重合時(如圖1),求∠BPD的度數;
(2)當BP在∠ABC的內部時(如圖2),求∠BPD的度數;
(3)當BP在∠ABC的外部時,請你直接寫出∠BPD的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系中,拋物線y=ax2+bx+c(a≠0)經過A(-1,0),B(3,0),C(0,3)三點,其頂點為D,連接BD,點是線段BD上一個動點(不與B、D重合),過點P作y軸的垂線,垂足為E,連接BE.
(1)求拋物線的解析式,并寫出頂點D的坐標;
(2)如果P點的坐標為(x,y),△PBE的面積為,求S與x的函數關系式,寫出自變量x的取值范圍,并求出S的最大值;
(3)在(2)的條件下,當S取得最大值時,過點P作x的垂線,垂足為F,連接EF,把△PEF沿直線EF折疊,點P的對應點為P′,請直接寫出P′點坐標,并判斷點P′是否在該拋物線上.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,已知∠BAC=45°,AD⊥BC于D,分別以AB、AC為對稱軸,畫出△ABD、△ACD的軸對稱圖形,D點的對稱點為E、F,延長EB、FC相交于G點,得到正方形AEGF(AE=EG=GF=AF,![]() ∠EAF=∠E=∠F=∠G=90°).
∠EAF=∠E=∠F=∠G=90°).

(1) 若AD=6,BD=2,求CG的長.
(2) 設BG=a,CG=b,BC=c.
①AE=_______.(用a、b、c表示)
②利用正方形面積驗證勾股定理![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數與形是數學中的兩個最古老,也是最基本的研究對象,它們在一定條件下可以互相轉化.樹形結合就是把抽象的數學語言、數量關系與直觀的幾何圖形、位置關系結合起來,通過“以形助數”或“以數解形”即通過抽象思維與形象思維的結合,可以使復雜問題簡單化,抽象問題具體化,從而起到優化解題途徑的目的.
(1) (思想應用)已知m, n均為正實數,且m+n=2求![]() 的最小值通過分析,愛思考的小明想到了利用下面的構造解決此問題:如圖, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,點E是線段AB上的動點,且不與端點重合,連接CE,DE,設AE=m, BE=n.
的最小值通過分析,愛思考的小明想到了利用下面的構造解決此問題:如圖, AB=2,AC=1,BD=2,AC⊥AB,BD⊥AB,點E是線段AB上的動點,且不與端點重合,連接CE,DE,設AE=m, BE=n.
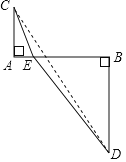
①用含m的代數式表示CE=_______, 用含n的代數式表示DE= ;
②據此求![]() 的最小值;
的最小值;
(2)(類比應用)根據上述的方法,求代數式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.將Rt△ABC繞點O依次旋轉90°、180°和270°,構成的圖形如圖所示.該圖是我國古代數學家趙爽制作的“勾股圓方圖”,也被稱作“趙爽弦圖”,它是我國最早對勾股定理證明的記載,也成為了2002年在北京召開的國際數學家大會的會標設計的主要依據.

(1)請利用這個圖形證明勾股定理;
(2)請利用這個圖形說明a2+b2≥2ab,并說明等號成立的條件;
(3)請根據(2)的結論解決下面的問題:長為x,寬為y的長方形,其周長為8,求當x,y取何值時,該長方形的面積最大?最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() 和
和![]() 的角平分線相交于點
的角平分線相交于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,過點
,過點![]() 作
作![]() 于
于![]() .下列五個結論:其中正確的有( )
.下列五個結論:其中正確的有( )
(1)![]() ;(2)
;(2)![]() ;(3)點
;(3)點![]() 到
到![]() 各邊的距離都相等;(4)設
各邊的距離都相等;(4)設![]() ,若
,若![]() ,則
,則![]() ;(5)
;(5)![]() .( )
.( )

A.2個B.3個C.4個D.5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com