
【題目】在平面直角坐標系中,點![]() 的坐標為
的坐標為![]() .
.
(1)如圖1,若點![]() 的坐標為
的坐標為![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,求
,求![]() 點坐標;
點坐標;

(2)如圖2,若點![]() 是
是![]() 的中點,求證:
的中點,求證:![]() ;
;

(3)如圖3,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() 是等邊三角形,連接
是等邊三角形,連接![]() ,若
,若![]() ,求
,求![]() 點坐標.
點坐標.

【答案】(1)(7,3);(2)見詳解;(3)(2,0).
【解析】
(1)過點C作CM⊥x軸于點M,由△ABC是等腰直角三角形,則AB=BC,然后證明△AOB≌△BMC,得到AO=BM,OB=CM,即可求出點C的坐標;
(2)根據題意,△ABO是直角三角形,點E是AB中點,即可得到![]() ;
;
(3)根據題意,把△DAO繞著點D旋轉60°得到△DCG,作CM⊥BG與M,則△DAO≌△DCG,得到∠AOD=∠CGD=30°,CG=OA=4,然后得到△ODG是等邊三角形,求出∠CGM=30°,得到![]() ,再由△AOB≌△BMC,得到OB=CM=2,即可得到點B的坐標.
,再由△AOB≌△BMC,得到OB=CM=2,即可得到點B的坐標.
解:(1)如圖,過點C作CM⊥x軸于點M,則∠BMC=90°=∠AOB,
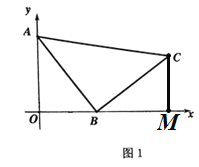
∵點A為(0,4),點B為(3,0),
∴OA=4,OB=3,
∵AB=BC,∠ABC=90°,
∴∠ABO+∠CBM=90°,∠BCM+∠CBM=90°,
∴∠ABO=∠BCM,
∴△AOB≌△BMC,
∴OA=BM,OB=CM=3,
∴OM=OB+BM=3+4=7,
∴點C的坐標為:(7,3);
(2)如圖,
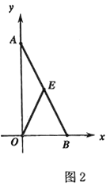
∵△AOB是直角三角形,點E是AB的中點,
∴OE=OA=OB=![]() ,
,
∴![]() ;
;
(3)根據題意,如圖,把△DAO繞著點D旋轉60°,得到△DCG,作CM⊥BG與M, 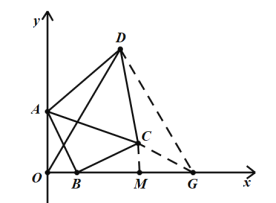
則△DAO≌△DCG,
∴∠AOD=∠CGD=30°,CG=OA=4,
∵OD=DG,∠ODG=60°,
∴△ODG是等邊三角形,
∴∠OGD=60°,
∴∠CGM=60°-30°=30°,
在Rt△CGM中,CM=![]() ,
,
由(1)知,△AOB≌△BMC,
∴OB=CM,
∴OB=2,
∴點B的坐標為:(2,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】設a,b是任意兩個不等實數,我們規定:滿足不等式a≤x≤b的實數x的所有取值的全體叫做閉區間,表示為[a,b].對于一個函數,如果它的自變量x與函數值y滿足:當m≤x≤n時,有m≤y≤n,我們就稱此函數是閉區間[m,n]上的“閉函數”.如函數y=﹣x+4,當x=1時,y=3;當x=3時,y=1,即當1≤x≤3時,恒有1≤y≤3,所以說函數y=﹣x+4是閉區間[1,3]上的“閉函數”,同理函數y=x也是閉區間[1,3]上的“閉函數”.
(1)反比例函數y=![]() 是閉區間[1,2018]上的“閉函數”嗎?請判斷并說明理由;
是閉區間[1,2018]上的“閉函數”嗎?請判斷并說明理由;
(2)如果已知二次函數y=x2﹣4x+k是閉區間[2,t]上的“閉函數”,求k和t的值;
(3)如果(2)所述的二次函數的圖象交y軸于C點,A為此二次函數圖象的頂點,B為直線x=1上的一點,當△ABC為直角三角形時,寫出點B的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象如圖所示,則下列結論:
的圖象如圖所示,則下列結論:
①![]() ,
,![]() 同號;②當
同號;②當![]() 和
和![]() 時,函數值相等;③
時,函數值相等;③![]() ;④當
;④當![]() 時,
時,![]() 的值只能取
的值只能取![]() ;⑤當
;⑤當![]() 時,
時,![]() .其中正確的有( )
.其中正確的有( )
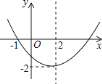
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為3的正方形ABCD中,點E、F分別在邊CD、AD上,且DE=AF=1,連接AE,BF交于點G,將△AED沿AE對折,得到△AEH,延長AH交CD于點P.
(1)求證:①△AED≌△BFA;②AE⊥BF;
(2)求S四邊形DEGF;
(3)求sin∠HPE的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,方格紙中每個小正方形的邊長都是1個單位長度.Rt△ABC的三個頂點A(﹣2,2),B(0,5),C(0,2).
(1)將△ABC以點C為旋轉中心旋轉180°,得到△A1B1C,請畫出的圖形△A1B1C.
(2)平移△ABC,使點A的對應點A2坐標為(﹣2,﹣6),請畫出平移后對應的△A2B2C2.
(3)請用無刻度的直尺在第一、四象限內畫出一個以A1B1為邊,面積是7的矩形A1B1EF.(保留作圖痕跡,不寫作法)
(4)若將△A1B1C繞某一點旋轉可得到△A2B2C2,請直接寫出旋轉中心的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A(1,a)是反比例函數![]() 的圖象上一點,直線
的圖象上一點,直線![]() 與反比例函數
與反比例函數![]() 的圖象的交點為點B、D,且B(3,﹣1),求:
的圖象的交點為點B、D,且B(3,﹣1),求:
(1)求反比例函數的解析式;
(2)求點D坐標,并直接寫出y1>y2時x的取值范圍;
(3)動點P(x,0)在x軸的正半軸上運動,當線段PA與線段PB之差達到最大時,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是一輛小汽車與墻平行停放的平面示意圖,汽車靠墻一側OB與墻MN平行且距離為0.8米,一輛小汽車車門寬AO為1.2米,當車門打開角度∠AOB為40°時,車門是否會碰到墻?______;(填“是”或“否”)請簡述你的理由_______.(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABD與△GDF都是等腰直角三角形,BD與DF均為斜邊(BD<DF).
(1)如圖1,B,D,F在同一直線上,過F作MF⊥GF于點F,取MF=AB,連結AM交BF于點H,連結GA,GM.
①求證:AH=HM;
②請判斷△GAM的形狀,并給予證明;
③請用等式表示線段AM,BD,DF的數量關系,并說明理由.
(2)如圖2,GD⊥BD,連結BF,取BF的中點H,連結AH并延長交DF于點M,請用等式直接寫出線段AM,BD,DF的數量關系.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com