【題目】如圖，在Rt△ABC中，∠C＝90°，BC＝6 cm，AC＝8 cm，將△BCD沿BD折疊，使點C落在AB邊的C′點處，那么△ADC′的面積是________．
【答案】6 cm2
【解析】
試題先根據勾股定理得到AB=10cm，再根據折疊的性質得到DC=DC′，BC=BC′=6cm，則AC′=4cm，設DC=xcm，在Rt△ADC′中根據勾股定理列方程求得x的值，然后根據三角形的面積公式計算即可．
∵∠C=90°，BC=6cm，AC=8cm，
∴AB=10cm，
∵將△BCD沿BD折疊，使點C落在AB邊的C′點，
∴△BCD≌△BC′D，
∴∠C=∠BC′D=90°，DC=DC′，BC=BC′=6cm，
∴AC′=AB-BC′=4cm，
設DC=xcm，則AD=（8-x）cm，
在Rt△ADC′中，AD2=AC′2+C′D2，
即（8-x）2=x2+42，解得x=3，
∵∠AC′D=90°，
∴△ADC′的面積═
×AC′×C′D=×4×3=6（cm2）．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖①，在正方形ABCD中，P是對角線AC上的一點，點E在BC的延長線上，且PE=PB．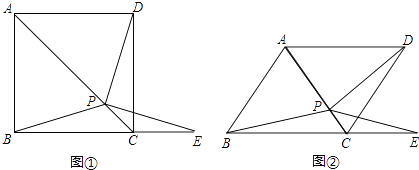 
（1）求證：△BCP≌△DCP；
（2）求證：∠DPE=∠ABC；
（3）把正方形ABCD改為菱形，其它條件不變（如圖②），若∠ABC=58°，則∠DPE=度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小東根據學習函數的經驗，對函數y= 
圖象與性質進行了探究，下面是小東的探究過程，請補充完整，并解決相關問題：
（1）函數y= 的自變量x的取值范圍是；
（2）如表是y與x的幾組對應值．
x | … | ﹣2 | ﹣1 | ﹣ | 0 | | 1 | | 2 | | 3 | 4 | … |
y | … | | | | 2 | | 4 | | 2 | | | m | … |
表中m的值為；
（3）如圖，在平面直角坐標系中，描出了以上表中各對對應值為坐標的點，根據描出的點，畫出函數y= 的大致圖象；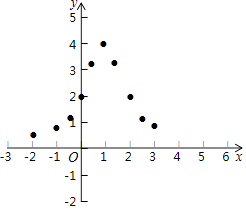 
（4）結合函數圖象，請寫出函數y= 
的一條性質.
（5）解決問題：如果函數y= 與直線y=a的交點有2個，那么a的取值范圍是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，在等腰直角三角形BCD中，∠BDC＝90°， BF平分∠DBC，與CD相交于點F，延長BD到A，使DA＝DF.
(1)求證：△FBD≌△ACD；
(2)延長BF交AC于點E，且BE⊥AC，求證：CE＝
BF；
(3)在(2)的條件下，H是BC邊的中點，連接DH，與BE相交于點G，如圖②. 試探索CE，GE，BG之間的數量關系，并證明你的結論．
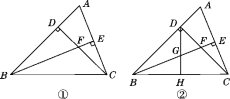
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AB=AC=2，∠BAC=45°，△AEF是由△ABC繞點A按逆時針方向旋轉得到的，連接BE、CF相交于點D．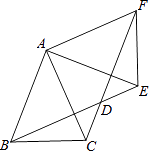 
（1）求證：BE=CF；
（2）當四邊形ABDF為菱形時，求CD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】⑴ 閱讀理解：我們知道在直角三角形中，有無數組勾股數，例如：5、12、13；9、40、41；……但其中也有一些特殊的勾股數，例如：3、4、5；是三個連續正整數組成的勾股數.
解決問題：① 在無數組勾股數中，是否存在三個連續偶數能組成勾股數？
答： ，若存在，試寫出一組勾股數： .
② 在無數組勾股數中，是否還存在其它的三個連續正整數能組成勾股數？若存在，求出勾股數，若不存在，說明理由.
③ 在無數組勾股數中，是否存在三個連續奇數能組成勾股數？若存在，求出勾股數，若不存在，說明理由.
⑵ 探索升華：是否存在銳角△ABC三邊也為連續正整數；且同時還滿足：∠B＞∠C＞∠A；∠ABC＝2∠BAC？若存在，求出△ABC三邊的長；若不存在，說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
