
如圖,已知正三角形ABC的邊長為2a.
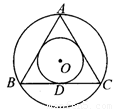
(1)求它的內切圓與外接圓組成的圓環(huán)的面積;
(2)根據(jù)計算結果,要求圓環(huán)的面積,只需測量哪一條弦的大小就可算出圓環(huán)的面積;
(3)將條件中的“正三角形”改為“正方形”“正六邊形”,你能得出怎樣的結論?
(4)已知正n邊形的邊長為2a,請寫出它的內切圓與外接圓組成的圓環(huán)面積.
(1)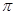 a2;(2)弦AB或BC或AC;
a2;(2)弦AB或BC或AC;
(3)圓環(huán)的面積均為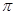 ·(
·(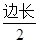 )2;(4)
)2;(4)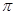 a2
a2
【解析】
試題分析:正多邊形的邊心距,半徑,邊長的一半正好構成直角三角形,根據(jù)勾股定理就可以求解.
(1)設正三角形ABC的中心為O,BC切⊙O于點D連接OB、OD,
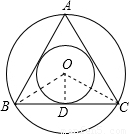
則OD⊥BC,BD=DC=a;
則S圓環(huán)=π•OB2-π•OD2=π(OB2-OD2)=π• BD2 =πa2.
(2)只需測出弦BC的長(或AC,AB).
(3)結果一樣,即S圓環(huán)=πa2
(4)S圓環(huán)=πa2.
考點:本題考查的是正多邊形的內切圓與外接圓,勾股定理
點評:正多邊形的計算,一般是過中心作邊的垂線,連接半徑,把內切圓半徑,外接圓半徑和高,中心角之間的計轉化為解直角三角形.


科目:初中數(shù)學 來源: 題型:
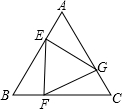 如圖,已知正三角形ABC的邊長為1,E,F(xiàn),G分別是AB,BC,CA上的點,且AE=BF=CG,設△EFG的面積為y,AE的長為x,則y關于x的函數(shù)的圖象大致是( )
如圖,已知正三角形ABC的邊長為1,E,F(xiàn),G分別是AB,BC,CA上的點,且AE=BF=CG,設△EFG的面積為y,AE的長為x,則y關于x的函數(shù)的圖象大致是( )A、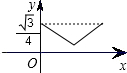 | B、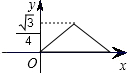 | C、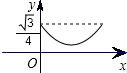 | D、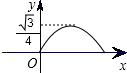 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 29、如圖,已知正三角形的邊長2a
29、如圖,已知正三角形的邊長2a查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
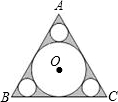 如圖,已知正三角形ABC的邊長為6,在△ABC中作內切圓O及三個角切圓(我們把與角兩邊及三角形內切圓都相切的圓叫角切圓),則△ABC的內切圓O的面積為
如圖,已知正三角形ABC的邊長為6,在△ABC中作內切圓O及三個角切圓(我們把與角兩邊及三角形內切圓都相切的圓叫角切圓),則△ABC的內切圓O的面積為查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
 點A運動.
點A運動.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:


查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com