
【題目】如圖,在平面直角坐標系中,![]() 為坐標原點,矩形
為坐標原點,矩形![]() 的頂點
的頂點![]() 、
、![]() ,將矩形
,將矩形![]() 的一個角
的一個角![]() 沿直線
沿直線![]() 折疊,使得點
折疊,使得點![]() 落在對角線
落在對角線![]() 上的點
上的點![]() 處,折痕與
處,折痕與![]() 軸交于點
軸交于點![]() .
.
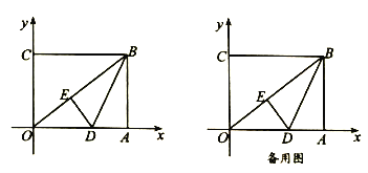
(1)線段![]() 的長度為__________;
的長度為__________;
(2)求直線![]() 所對應的函數解析式;
所對應的函數解析式;
(3)若點![]() 在線段
在線段![]() 上,在線段
上,在線段![]() 上是否存在點
上是否存在點![]() ,使四邊形
,使四邊形![]() 是平行四邊形?若存在,請求出點
是平行四邊形?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)15;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根據勾股定理即可解決問題;
(2)設AD=x,則OD=OA=AD=12-x,根據軸對稱的性質,DE=x,BE=AB=9,又OB=15,可得OE=OB-BE=15-9=6,在Rt△OED中,根據OE2+DE2=OD2,構建方程即可解決問題;
(3)過點E作EP∥BD交BC于點P,過點P作PQ∥DE交BD于點Q,則四邊形DEPQ是平行四邊形,再過點E作EF⊥OD于點F,想辦法求出最小PE的解析式即可解決問題。
解:(1)在Rt△ABC中,∵OA=12,AB=9,
![]()
故答案為15.
(2)如圖,
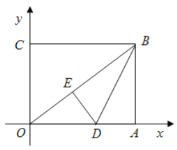
設![]() ,則
,則![]()
根據軸對稱的性質,![]() ,
,
又![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,則
,則![]() ,
,
∴![]() ,
,
∴![]()
設直線![]() 所對應的函數表達式為:
所對應的函數表達式為:![]()
則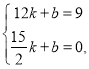 ,
,
解得![]()
∴直線![]() 所對應的函數表達式為:
所對應的函數表達式為:![]() .
.
故答案為:![]()
(3)過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,則四邊形
,則四邊形![]() 是平行四邊形,再過點
是平行四邊形,再過點![]() 作
作![]() 于點
于點![]() ,
,
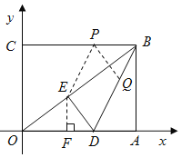
由![]()
得![]() ,即點
,即點![]() 的縱坐標為
的縱坐標為![]() ,
,
又點![]() 在直線
在直線![]() :
:![]() 上,
上,
∴![]() ,解得
,解得![]() ,
,
![]()
由于![]() ,所以可設直線
,所以可設直線![]() ,
,
∵![]() 在直線
在直線![]() 上
上
∴![]() ,解得
,解得![]()
∴直線![]() 為
為![]() ,
,
令![]() ,則
,則![]() ,解得
,解得![]() ,
,
∴![]()


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,將菱形紙片ABCD折疊,使點A恰好落在菱形的對稱中心O處,折痕為EF,若菱形ABCD的邊長為2cm,∠A=120°,則EF的長為( )
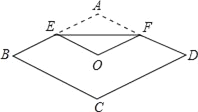
A. 2![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,記
中,記![]() 與
與![]() 的函數
的函數![]() (
(![]() ≠0,n≠0)的圖象為圖形G, 已知圖形G與
≠0,n≠0)的圖象為圖形G, 已知圖形G與![]() 軸交于點
軸交于點![]() ,當
,當![]() 時,函數
時,函數![]() 有最小(或最大)值n, 點B的坐標為(
有最小(或最大)值n, 點B的坐標為(![]() ,
, ![]() ),點A、B關于原點O的對稱點分別為C、D,若A、B、C、D中任何三點都不在一直線上,且對角線AC,BD的交點與原點O重合,則稱四邊形ABCD為圖形G的伴隨四邊形,直線AB為圖形G的伴隨直線.
),點A、B關于原點O的對稱點分別為C、D,若A、B、C、D中任何三點都不在一直線上,且對角線AC,BD的交點與原點O重合,則稱四邊形ABCD為圖形G的伴隨四邊形,直線AB為圖形G的伴隨直線.

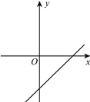
(1)如圖,若函數![]() 的圖象記為圖形G,求圖形G的伴隨直線的表達式;
的圖象記為圖形G,求圖形G的伴隨直線的表達式;
(2)如圖,若圖形G的伴隨直線的表達式是![]() ,且伴隨四邊形的面積為12,求
,且伴隨四邊形的面積為12,求![]() 與
與![]() 的函數
的函數![]() (m>0,n <0)的表達式;
(m>0,n <0)的表達式;
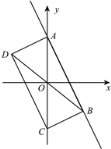
(3)如圖,若圖形G的伴隨直線是![]() ,且伴隨四邊形ABCD是矩形,求點B的坐標.
,且伴隨四邊形ABCD是矩形,求點B的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司開發處一款新的節能產品,該產品的成本價為6元/件,該產品在正式投放市場前通過代銷點進行了為期一個月(30天)的試銷售,售價為10元/件,工作人員對銷售情況進行了跟蹤記錄,并將記錄情況繪制成圖象,圖中的折線ABC表示日銷售量y(件)與銷售時間x(天)之間的函數關系.
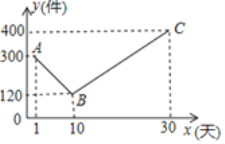
(1)求y與x之間的函數表達式,并寫出x的取值范圍;
(2)若該節能產品的日銷售利潤為W(元),求W與x之間的函數表達式,并求出日銷售利潤不超過1040元的天數共有多少天?
(3)若5≤x≤17,直接寫出第幾天的日銷售利潤最大,最大日銷售利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
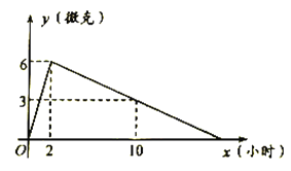
【題目】某醫藥研究所開發了一種新藥,在試驗效果時發現,如果成人按規定劑量服用,服藥后血液中的含藥量逐漸增多,一段時間后達到最大值,接著藥量逐步衰減直至血液中含藥量為0,每毫升血液中含藥量![]() (微克)隨時間
(微克)隨時間![]() (小時)的變化如圖所示,下列說法:(1)2小時血液中含藥量最高,達每毫升6微克.(2)每毫升血液中含藥量不低于4微克的時間持續達到了6小時.(3)如果一病人下午6:00按規定劑量服此藥,那么,第二天中午12:00,血液中不再含有該藥,其中正確說法的個數是()
(小時)的變化如圖所示,下列說法:(1)2小時血液中含藥量最高,達每毫升6微克.(2)每毫升血液中含藥量不低于4微克的時間持續達到了6小時.(3)如果一病人下午6:00按規定劑量服此藥,那么,第二天中午12:00,血液中不再含有該藥,其中正確說法的個數是()
A. 0B. 1
C. 2D. 3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】勾股定理神秘而美妙,它的證法多樣,其中的“面積法”給了李明靈感,他驚喜地發現;當兩個全等的直角三角形如圖(1)擺放時可以利用面積法”來證明勾股定理,過程如下
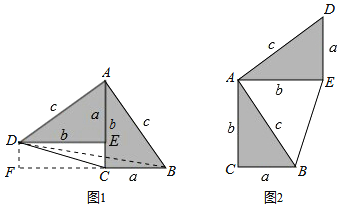
如圖(1)∠DAB=90°,求證:a2+b2=c2
證明:連接DB,過點D作DF⊥BC交BC的延長線于點F,則DF=b-a
S四邊形ADCB=![]()
S四邊形ADCB=![]()
∴![]() 化簡得:a2+b2=c2
化簡得:a2+b2=c2
請參照上述證法,利用“面積法”完成如圖(2)的勾股定理的證明,如圖(2)中∠DAB=90°,求證:a2+b2=c2
查看答案和解析>>
科目:初中數學 來源: 題型:
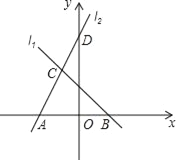
【題目】如圖,直線l1的解析式為y=﹣x+2,l1與x軸交于點B,直線l2經過點D(0,5),與直線l1交于點C(﹣1,m),且與x軸交于點A,
(1)求點C的坐標及直線l2的解析式;
(2)求△ABC的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com