
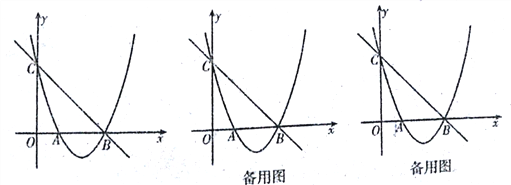
【題目】如圖,在平面直角坐標系xOy中,點O為坐標原點,拋物線![]() 與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,點B的坐標為(3,0),直線
與x軸交于A、B兩點(點A在點B的左側),與y軸交于點C,點B的坐標為(3,0),直線![]() 經過B、C兩點.
經過B、C兩點.
(1)求拋物線的解析式;
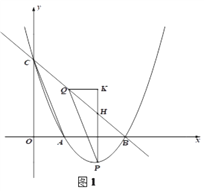
(2)點P是x軸下方拋物線上一點,連接AC,過點P作PQ∥AC交BC于點Q,過點Q作x軸的平行線,過點P作y軸的平行線,兩條直線相交于點K,PK交BC于點H,設QK的長為t,PH的長為d,求d與t之間的函數關系式;(不要求寫出自變量t的取值范圍)
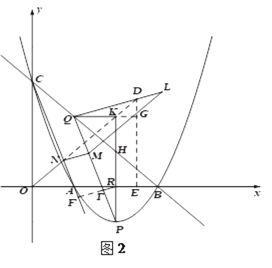
(3)在(2)的條件下,PK交x軸于點R,過點R作RT⊥PQ,垂足為T,當PK=![]() PT時,將線段QT繞點Q逆時針旋轉90
PT時,將線段QT繞點Q逆時針旋轉90![]() 得到線段QL,M是線段PQ上一動點,過點M作直線AC的垂線,垂足為N,連接ON、ML,當ML∥ON時,求N點坐標.
得到線段QL,M是線段PQ上一動點,過點M作直線AC的垂線,垂足為N,連接ON、ML,當ML∥ON時,求N點坐標.
【答案】(1)y=![]() -4x+3(2)
-4x+3(2)![]() (3)
(3)![]()
【解析】試題分析:
(1)由已知條件易得點C的坐標為(0,3),把B、C兩點坐標代入二次函數的解析式可求得b、c的值,即可得到二次函數的解析式;
(2)由(1)中所求二次函數的解析式易得點A的坐標為(1,0),結合點C(0,3)的坐標可得tan∠ACO=![]() ,由OB=OC易得∠OCB=∠OBC=45°,結合PK∥y軸,QK∥x軸可得∠KHQ=∠KQH=45°,由此可得KH=QK=t,由PQ∥AC可得∠ACB=∠PQB,結合∠OCB=∠PHB=∠PQB+∠QPK,可得∠QPK=∠ACO,則tan∠QPK=
,由OB=OC易得∠OCB=∠OBC=45°,結合PK∥y軸,QK∥x軸可得∠KHQ=∠KQH=45°,由此可得KH=QK=t,由PQ∥AC可得∠ACB=∠PQB,結合∠OCB=∠PHB=∠PQB+∠QPK,可得∠QPK=∠ACO,則tan∠QPK=![]() ,由此可得d=2t;
,由此可得d=2t;
(3)如下圖2,延長![]() 交
交![]() 于點
于點![]() ,延長
,延長![]() 交直線
交直線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,先由已知條件解PR=t,OR=3-t,由此可得點P的坐標為(3-t,-t),將點P的坐標代入
,先由已知條件解PR=t,OR=3-t,由此可得點P的坐標為(3-t,-t),將點P的坐標代入![]() 解得t1=0(舍去),t2=1,由此可得
解得t1=0(舍去),t2=1,由此可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ;結合已知條件進一步可求得點D的坐標為
;結合已知條件進一步可求得點D的坐標為![]() ,由此即可求得直線OD的解析式為y=x,再由已知求出直線AC的解析式即可由此求出直線OD和AC的交點N的坐標了.
,由此即可求得直線OD的解析式為y=x,再由已知求出直線AC的解析式即可由此求出直線OD和AC的交點N的坐標了.
試題分析:
(1)把x=0代入y=-x+3,得y=3,![]()
![]()
∵拋物線![]() 經過
經過![]()
![]() ,
, ![]()
![]()
∴![]() 解得
解得![]()
∴![]() ,
, ![]()
∴拋物線為y=![]() -4x+3
-4x+3
(2)如下圖1,令![]() ,即
,即![]() ,解得
,解得![]() ,∴
,∴ ![]() 點坐標為
點坐標為![]() ,∴
,∴ ![]() ,∵
,∵ ![]() 點坐標為
點坐標為![]() ,∴
,∴ ![]() ,∴
,∴![]()
∵![]()
![]() ,
, ![]()
![]() ,∴
,∴ ![]() , ∴
, ∴![]() , ∵
, ∵![]() 軸,
軸,
∴![]() ,∵
,∵ ![]() 軸,
軸, ![]() 軸,∴
軸,∴![]() ,
,
∴![]() ,∴
,∴ ![]()
∵![]() ,∴
,∴ ![]() ,∵
,∵ ![]() ,
,
∴![]() ,
,
即![]() ∴
∴![]() , ∵
, ∵![]() ,
,
∴![]() span>
span>
∵![]() ,∴
,∴ ![]() ;
;
(3)如下圖2,延長![]() 交
交![]() 于點
于點![]() ,延長
,延長![]() 交直線
交直線![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() ,延長
,延長![]() 交
交![]() 于點
于點![]() ,
,
∵![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]()
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
將![]() 代入
代入![]() 中得,
中得, ![]() ,
,
解得![]() (舍),
(舍), ![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,由題意知,四邊形
,由題意知,四邊形![]() 是矩形,
是矩形,
∴![]() ,
,
由旋轉知, ![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四邊形![]() 是平行四邊形,
是平行四邊形,
∴![]() ,
, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
, ![]() ,
,
∴![]()
∴![]() ,
,
∵![]()
∴![]() ,
, ![]() ,由題意知四邊形
,由題意知四邊形![]() 為矩形,
為矩形, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
∴![]()
設直線![]() 的解析式為
的解析式為![]() ,將
,將![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() ,設直線
,設直線![]() 的解析式為
的解析式為![]() ,將
,將![]() ,
, ![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
∴直線![]() 的解析式為
的解析式為![]() ,令
,令![]() ,解得
,解得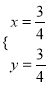 ,
,
∴![]() 點坐標為
點坐標為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系中,正方形OABC的頂點O與原點重合,頂點A,C分別在x軸,y軸上,反比例函數的圖象與正方形的兩邊AB,BC分別交于點M,N,ND⊥x軸,垂足為D,連接OM,ON,MN.下列結論:①△OCN≌△OAM;②ON=MN;③四邊形DAMN與△MON面積相等;④若∠MON=45°,MN=2,則點C的坐標為(0, ![]() +1).其中正確結論的序號是____________.
+1).其中正確結論的序號是____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,□ABCD的對角線AC、BD相交于點O,AE=CF.
(1)求證:△BOE≌△DOF;
(2)若BD=EF,連接DE、BF,判斷四邊形EBFD的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
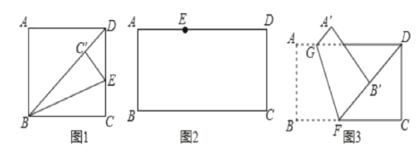
【題目】(1)如圖1,將矩形ABCD折疊,使BC落在對角線BD上,折痕為BE,點C落在點C'處,若∠ADB=46°,則∠DBE的度數為______.
(2)小明手中有一張矩形紙片ABCD,AB=4,AD=9.
(畫一畫)
如圖2,點E在這張矩形紙片的邊AD上,將紙片折疊,使AB落在CE所在直線上,折痕設為MN(點M,N分別在邊AD,BC上),利用直尺和圓規畫出折痕MN(不寫作法,保留作圖痕跡,并用黑色水筆把線段描清楚);
(算一算)
如圖3,點F在這張矩形紙片的邊BC上,將紙片折疊,使FB落在射線FD上,折痕為GF,點A,B分別落在點A',B'處,若AG=![]() ,求B'D的長;
,求B'D的長;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形OABC的頂點A. C分別在x、y軸的正半軸上,點D為BC邊上的點,反比例函數y=![]() (k≠0)在第一象限內的圖象經過點D(m,2)和AB邊上的點E(3,
(k≠0)在第一象限內的圖象經過點D(m,2)和AB邊上的點E(3,![]() ).
).
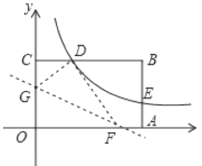
(1)求反比例函數的表達式和m的值;
(2)將矩形OABC的進行折疊,使點O于點D重合,折痕分別與x軸、y軸正半軸交于點F,G,求折痕FG所在直線的函數關系式。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某高中學校為使高一新生入校后及時穿上合身的校服,現提前對某校九年級(3)班學生即將所穿校服型號情況進行了摸底調查,并根據調查結果繪制了如圖兩個不完整的統計圖(校服型號以身高作為標準,共分為6種型號).
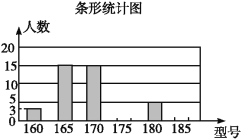
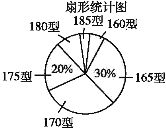
根據以上信息,解答下列問題:
(1)該班共有 名學生?其中穿175型校服的學生有 人.
(2)在條形統計圖中,請把空缺的部分補充完整;
(3)在扇形統計圖中,請計算185型校服所對應扇形圓心角度數為 ;
(4)該班學生所穿校服型號的眾數是 ,中位數是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
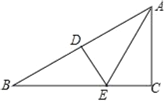
【題目】如圖,在△ABC中,∠B=30°,邊AB的垂直平分線分別交AB和BC于點D,E,且AE平分∠BAC.
(1)求∠C的度數;
(2)若CE=1,求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲乙兩家綠化養護公司各自推出了校園綠化養護服務的收費方案.
甲公司方案:每月的養護費用y(元)與綠化面積x(平方米)是一次函數關系,如圖所示.
乙公司方案:綠化面積不超過1000平方米時,每月收取費用5500元;綠化面積超過1000平方米時,每月在收取5500元的基礎上,超過部分每平方米收取4元.

(1)求如圖所示的y與x的函數解析式;(不要求寫取值范圍)
(2)如果某學校目前的綠化面積是1200平方米.試通過計算說明:選擇哪家公司的服務,每月的綠化養護費用較少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com