【題目】已知：在平行四邊形ABCD中，AE⊥BC，垂足為E，CE=CD，點F為CE的中點，點G為CD上的一點，連接DF，EG，AG，∠1=∠2．
（1）求證：G為CD的中點.
(2) 若CF=2，AE=3，求BE的長；
【答案】(1)詳見解析；（2）
.
【解析】試題分析：（1）通過證△ECG≌△DCF得到CG=CF，結合已知條件知CG=
CD，即G為CD的中點．
（2）求出DC=CE=2CF=4，求出AB，根據勾股定理求出BE即可．
試題解析：(1)證明：如圖，∵點F為CE的中點，
∴CF=
CE
在△ECG與△DCF中，
∠2=∠1、∠C=∠C、CE=CD，
∴△ECG≌△DCF(AAS)，
∴CG=CF=
CE.
又CE=CD，
∴CG=
CD，即G為CD的中點；
(2)∵CE=CD，點F為CE的中點，CF=2，
∴DC=CE=2CF=4，
∵四邊形ABCD是平行四邊形，
∴AB=CD=4，
∵AE⊥BC，
∴∠AEB=90，
在Rt△ABE中,由勾股定理得：BE=
科目：初中數學 來源： 題型：
【題目】（本題6分）某市對一大型超市銷售的甲、乙、丙3種大米進行質量檢測．共抽查大米200袋，質量評定分為A、B兩個等級（A級優于B級），相應數據的統計圖如下：
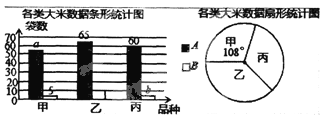
根據所給信息，解決下列問題：
(1)a＝_______，b＝_______．
(2)已知該超市現有乙種大米750袋，根據檢測結果，請你估計該超市乙種大米中有多少袋B級大米？
(3)對于該超市的甲種和丙種大米，你會選擇購買哪一種？請簡述理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了抓住文化藝術節的商機，某商店決定購進A、B兩種藝術節紀念品．若購進A種紀念品8件，B種紀念品3件，需要950元；若購進A種紀念品5件，B種紀念品6件，需要800元．
（1）求購進A、B兩種紀念品每件各需多少元？
（2）若該商店決定購進這兩種紀念品共100件，考慮市場需求和資金周轉，用于購買這100件紀念品的資金不超過8 000元，那么該商店至多購進A種紀念品幾件？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把一張矩形的紙ABCD沿對角線BD折疊，使點C落在點E處，BE與AD交于點F．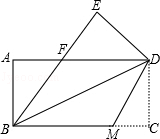 
（1）求證：△ABF≌△EDF；
（2）若將折疊的圖形恢復原狀，點F與BC邊上的點M正好重合，連接DM，試判斷四邊形BMDF的形狀，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點C在線段AB上，點M、N分別是AC、BC的中點.
（1）若AC ＝9cm，CB ＝ 6 cm，求線段MN的長；
（2）若C為線段AB上任一點，滿足AC＋CB ＝
cm，其它條件不變，你能猜想MN的長度嗎？并說明理由.你能用一句簡潔的話描述你發現的結論嗎？
（3）若C在線段AB的延長線上，且滿足AC
BC ＝ b cm，M、N分別為AC、BC的中點，你能猜想MN的長度嗎？請畫出圖形，寫出你的結論，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀與理解：
如圖，一只甲蟲在5×5的方格（每個方格邊長均為1）上沿著網格線爬行．若我們規定：在如圖網格中，向上（或向右） 爬行記為“+”，向下（或向左） 爬行記為“﹣”，并且第一個數表示左右方向，第二個數表示上下方向．
例如：從A到B記為：A→B（+1，+4），從D到C記為：D→C（﹣1，+2）．
思考與應用：
（1）圖中A→C（ ， ），B→C（ ， ），D→A（ ， ）
（2）若甲蟲從A到P的行走路線依次為：（+3，+2）→（+1，+3）→（+1，﹣2），請在圖中標出P的位置．
（3）若甲蟲的行走路線為A→（+1，+4）→（+2，0）→（+1，﹣2）→（﹣4，﹣2），請計算該甲蟲走過的總路程．
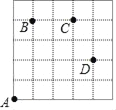
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，動點P在平面直角坐標系中按圖中箭頭所示方向運動，第1次從原點運動到點
，第2次接著運動到點
，第3次接著運動到點
，
按這樣的運動規律，經過第2017次運動后，動點P的坐標是______，經過第2018次運動后，動點P的坐標是______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀以下材料： 2017年1月28日至2月1日農歷正月初一至初五，平谷區政府在占地面積6萬平方米的琴湖公園舉辦主題為“逛平谷廟會樂百姓生活”的平谷區首屆春節廟會．
本次廟會共設置了文藝展演區、非遺展示互動區、特色商品區、兒童娛樂游藝區、特色美食區等五個不同主題的展區．展區總面積1720平方米．文藝展演區占地面積600平方米，占展區總面積的34.9%；非遺展示區占地190平方米，占展區總面積的11.0%；特色商品區占地面積是文藝展演區的一半，占展區總面積的17.4%；特色美食區占地200平方米，占展區總面積的11.6%；還有孩子們喜愛的兒童娛樂游藝區．
此次廟會本著弘揚、挖掘、展示平谷春節及民俗文化，以京津冀不同地域的特色文化為出發點，全面展示平谷風土人情及津冀人文特色．大年初一，來自全國各地的約3.2萬人踏著新春的腳步，揭開了首屆平谷廟會的帷幕．大年初二盡管天氣寒冷，市民逛廟會熱情不減，又約有4.3萬人次參觀了廟會，品嘗特色美食，觀看綠都古韻、秧歌表演、天橋絕活，一路猜燈謎、賞圖片展，場面火爆．琳瑯滿目的泥塑、木版畫、剪紙、年畫等民俗作品也讓游客愛不釋手，紛紛購買．大年初三，單日接待游客約4萬人次，大年初四風和日麗的天氣讓廟會進入游園高峰，單日接待量較前日增長了約50%．大年初五，活動進入尾聲，但廟會現場仍然人頭攢動，仍約有5.5萬人次來園參觀．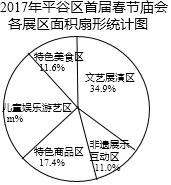
（1）直接寫出扇形統計圖中m的值；
（2）初四這天，廟會接待游客量約萬人次；
（3）請用統計圖或統計表，將廟會期間每日接待游客的人數表示出來．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，OA，OD是⊙O半徑，過A作⊙O的切線，交∠AOD的平分線于點C，連接CD，延長AO交⊙O于點E，交CD的延長線于點B 
（1）求證：直線CD是⊙O的切線；
（2）如果D點是BC的中點，⊙O的半徑為3cm，求 
的長度（結果保留π）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com