
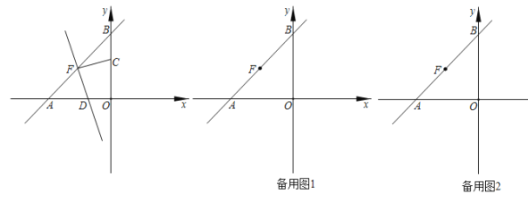
【題目】如圖,已知直線![]() 經過點
經過點![]() ,交x軸于點A,y軸于點B,F為線段AB的中點,動點C從原點出發,以每秒1個位長度的速度沿y軸正方向運動,連接FC,過點F作直線FC的垂線交x軸于點D,設點C的運動時間為t秒.
,交x軸于點A,y軸于點B,F為線段AB的中點,動點C從原點出發,以每秒1個位長度的速度沿y軸正方向運動,連接FC,過點F作直線FC的垂線交x軸于點D,設點C的運動時間為t秒.
![]() 當
當![]() 時,求證:
時,求證:![]() ;
;
![]() 連接CD,若
連接CD,若![]() 的面積為S,求出S與t的函數關系式;
的面積為S,求出S與t的函數關系式;
![]() 在運動過程中,直線CF交x軸的負半軸于點G,
在運動過程中,直線CF交x軸的負半軸于點G,![]() 是否為定值?若是,請求出這個定值;若不是,請說明理由.
是否為定值?若是,請求出這個定值;若不是,請說明理由.
【答案】(1)見解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)連接OF,根據“直線![]() 經過點
經過點![]() ”可得k=1,進而求出A(﹣4,0),B(0,4),得出△AOB是等腰直角三角形,得出∠CBF=45°,得出OF=
”可得k=1,進而求出A(﹣4,0),B(0,4),得出△AOB是等腰直角三角形,得出∠CBF=45°,得出OF=![]() AB=BF,OF⊥AB,得出∠OFD=∠BFC,證得△BCF≌△ODF,即可得出結論
AB=BF,OF⊥AB,得出∠OFD=∠BFC,證得△BCF≌△ODF,即可得出結論
(2)①根據全等三角形的性質可得出0<t<4時,BC=OD=t﹣4,再根據勾股定理得出CD2=2t2-8t+16,證得△FDC是等腰直角三角形,得出![]() ,即可得出結果;
,即可得出結果;
②同理當t≥4時,得出BC=OD=t﹣4,由勾股定理得出CD2=OD2+OC2=2t2﹣8t+16,證出△FDC是等腰直角三角形,得出FC2![]() CD2,即可得出結果;
CD2,即可得出結果;
(3)由待定系數法求出直線CF的解析式,當y=0時,可得出G![]() ,因此OG
,因此OG![]() ,求出
,求出![]() 即可.
即可.
![]() 證明:連接OF,如圖1所示:
證明:連接OF,如圖1所示:

![]() 直線
直線![]() 經過點
經過點![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 直線
直線![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ;
;
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() 為線段AB的中點,
為線段AB的中點,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,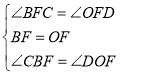 ,
,
![]() ≌
≌![]() ,
,
![]() ;
;
![]() 解:
解:![]() 當
當![]() 時,連接OF,如圖2所示:
時,連接OF,如圖2所示:
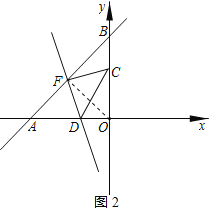
由題意得:![]() ,
,![]() ,
,
由![]() 得:
得:![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() 的面積
的面積![]() ;
;
![]() 當
當![]() 時,連接OF,如圖3所示:
時,連接OF,如圖3所示:
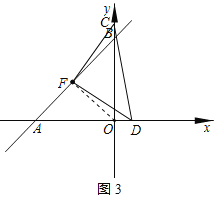
由題意得:![]() ,
,![]() ,
,
由![]() 得:
得:![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,
![]() 的面積
的面積![]() ;
;
綜上所述,S與t的函數關系式為![]() ;
;
![]() 解:
解:![]() 為定值
為定值![]() ;理由如下:
;理由如下:
![]() 當
當![]() 時,如圖4所示:
時,如圖4所示:
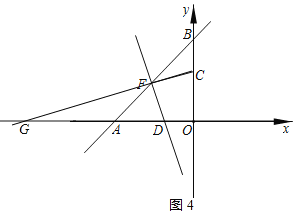
當設直線CF的解析式為![]() ,
,
![]() ,
,![]() ,F為線段AB的中點,
,F為線段AB的中點,
![]() ,
,
把點![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
![]() 直線CF的解析式為
直線CF的解析式為![]() ,
,
當![]() 時,
時,![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 當
當![]() 時,如圖5所示:
時,如圖5所示:
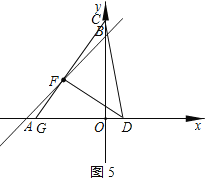
同![]() 得:
得:![]() ;
;
綜上所述,![]() 為定值
為定值![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知:方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,點C的坐標為(4,-1).
(1)請以y軸為對稱軸,畫出與△ABC對稱的△A1B1C1,并直接寫出點A1、B1、C1的坐標;
(2)△ABC的面積是 .
(3)點P(a+1,b-1)與點C關于x軸對稱,則a= ,b= .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣x2+![]() x+2與直線y=
x+2與直線y=![]() x+2相交于點C和D,點P是拋物線在第一象限內的點,它的橫坐標為m,過點P作PE⊥x軸,交CD于點F.
x+2相交于點C和D,點P是拋物線在第一象限內的點,它的橫坐標為m,過點P作PE⊥x軸,交CD于點F.
(1)求點C和D的坐標;
(2)求拋物線與x軸的交點坐標;
(3)如果以P、C、O、F為頂點的四邊形是平行四邊形,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,真命題的是( )
A.兩邊和一角對應相等,兩三角形全等
B.兩腰對應相等的兩等腰三角形全等
C.兩角和一邊對應相等,兩三角形全等
D.兩銳角對應相等的兩直角三角形全等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,AC,BD是對角線,將△DCB繞著點D順時針旋轉45°得到△DGH,HG交AB于點E,連接DE交AC于點F,連接FG.則下列結論:
①四邊形AEGF是菱形;②△HED的面積是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正確的結論是( )
.其中正確的結論是( )
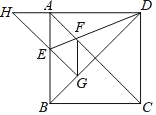
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖一,在平面直角坐標系中,![]() 是
是![]() 軸正半軸上一點,
軸正半軸上一點,![]() 是第四象限一點,
是第四象限一點,![]() 軸,交
軸,交![]() 軸負半軸于
軸負半軸于![]() ,且(a-2)+|b+3|=0,
,且(a-2)+|b+3|=0,![]() 四邊形AOBC=12.
四邊形AOBC=12.
(1)求![]() 點坐標
點坐標
(2)如圖二,設![]() 為線段
為線段![]() 上一動點(點
上一動點(點![]() 不與點
不與點![]() 重合),求證:∠ADB+∠DBC-∠OAD=180°
重合),求證:∠ADB+∠DBC-∠OAD=180°
(3)如圖三,當![]() 點在線段
點在線段![]() 上運動(點
上運動(點![]() 不與點
不與點![]() 重合),
重合),![]() 點在線段
點在線段![]() 上運動(點
上運動(點![]() 不與點
不與點![]() 重合)時,連接
重合)時,連接![]() 、
、![]() 作∠OAD、∠DEB的平分線交于
作∠OAD、∠DEB的平分線交于![]() 點,請你探索∠AFE與∠ADE之間的關系,并說明理由.
點,請你探索∠AFE與∠ADE之間的關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD⊥AB,垂足為H,連接AC,過![]() 上一點E作EG∥AC交CD的延長線于點G,連接AE交CD于點F,且EG=FG.
上一點E作EG∥AC交CD的延長線于點G,連接AE交CD于點F,且EG=FG.
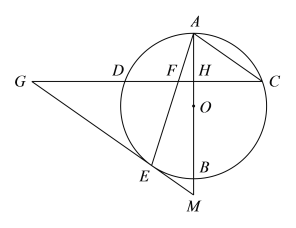
(1)求證:EG是⊙O的切線;
(2)延長AB交GE的延長線于點M,若AH=2,![]() ,求OM的長.
,求OM的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】材料閱讀:
若a是正整數,則長度為![]() 的線段是有可能表示正方形網格中兩個格點之間的距離(設小正方形的長度為單位1).如圖1所示,A、B兩點之間的距離就是
的線段是有可能表示正方形網格中兩個格點之間的距離(設小正方形的長度為單位1).如圖1所示,A、B兩點之間的距離就是![]() .
.

(1)在圖1中以A為一個端點,畫出一條長為![]() 的線段AC;
的線段AC;
(2)![]() (空格處填正整數,兩組數要求不一樣),并根據你填的數字,在圖2中畫出兩種對應的線段,其長度均為
(空格處填正整數,兩組數要求不一樣),并根據你填的數字,在圖2中畫出兩種對應的線段,其長度均為![]() ;
;
(3)利用材料所給的方法,直接寫出三邊長分別為![]() 、
、![]() 、
、![]() 的三角形的面積:__________.
的三角形的面積:__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:平面直角坐標系中,點A(a,b)的坐標滿足|a﹣b|+b2﹣8b+16=0.

(1)如圖1,求證:OA是第一象限的角平分線;
(2)如圖2,過A作OA的垂線,交x軸正半軸于點B,點M、N分別從O、A兩點同時出發,在線段OA上以相同的速度相向運動(不包括點O和點A),過A作AE⊥BM交x軸于點E,連BM、NE,猜想∠ONE與∠NEA之間有何確定的數量關系,并證明你的猜想;
(3)如圖3,F是y軸正半軸上一個動點,連接FA,過點A作AE⊥AF交x軸正半軸于點E,連接EF,過點F點作∠OFE的角平分線交OA于點H,過點H作HK⊥x軸于點K,求2HK+EF的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com