
【題目】已知A、B、C三地在同一條路上,A地在B地的正南方3千米處,甲、乙兩人分別從A、B兩地向正北方向的目的地C勻速直行,他們分別和A地的距離s(千米)與所用的時間t(小時)的函數關系如圖所示.

(1)圖中的線段l1是 (填“甲”或“乙”)的函數圖象,C地在B地的正北方向 千米處;
(2)誰先到達C地?并求出甲乙兩人到達C地的時間差;
(3)如果速度慢的人在兩人相遇后立刻提速,并且比先到者晚1小時到達C地,求他提速后的速度.
【答案】(1)乙;3;(2)甲先到達,到達目的地的時間差為![]() 小時;(3)速度慢的人提速后的速度為
小時;(3)速度慢的人提速后的速度為![]() 千米/小時.
千米/小時.
【解析】分析:
(1)根據題意結合所給函數圖象進行判斷即可;
(2)由所給函數圖象中的信息先求出二人所對應的函數解析式,再由解析式結合圖中信息求出二人到達C地的時間并進行比較、判斷即可得到本問答案;
(3)根據圖象中的信息結合(2)中的結論進行解答即可.
詳解:
(1)由題意結合圖象中的信息可知:圖中線段l1是乙的圖象;C地在B地的正北方6-3=3(千米)處.
(2)甲先到達.
設甲的函數解析式為s=kt,則有4=t,
∴s=4t.
∴當s=6時,t=![]() .
.
設乙的函數解析式為s=nt+3,則有4=n+3,即n=1.
∴乙的函數解析式為s=t+3.
∴當s=6時,t=3.
∴甲、乙到達目的地的時間差為:![]() (小時).
(小時).
(3)設提速后乙的速度為v千米/小時,
∵相遇處距離A地4千米,而C地距A地6千米,
∴相遇后需行2千米.
又∵原來相遇后乙行2小時才到達C地,
∴乙提速后2千米應用時1.5小時.
即![]() ,解得:
,解得:![]() ,
,
答:速度慢的人提速后的速度為![]() 千米/小時.
千米/小時.


科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為6,B是數軸上一點,且AB=10,動點P從點A出發,以每秒6個單位長度的速度沿數軸向左勻速運動,設運動時間為t(t>0)秒,
(1)寫出數軸上點B所表示的數 ;
(2)點P所表示的數 ;(用含t的代數式表示);
(3)M是AP的中點,N為PB的中點,點P在運動的過程中,線段MN的長度是否發生變化?若變化,說明理由;若不變,請你畫出圖形,并求出線段MN的長.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某品牌T恤專營批發店的T恤衫在進價基礎上加價m%銷售,每月銷售額9萬元,該店每月固定支出1.7萬元,進貨時還需付進價5%的其它費用.
(1)為保證每月有1萬元的利潤,m的最小值是多少?(月利潤=總銷售額-總進價-固定支
出-其它費用)
(2)經市場調研發現,售價每降低1%,銷售量將提高6%,該店決定自下月起降價以促進銷售,已知每件T恤原銷售價為60元,問:在m取(1)中的最小值且所進T恤當月能夠全部銷售完的情況下,銷售價調整為多少時能獲得最大利潤,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索代數式![]() 與代數式
與代數式![]() 的關系.
的關系.
(1)當![]() ,
,![]() 時,分別計算兩個代數式的值.
時,分別計算兩個代數式的值.
(2)當![]() ,
,![]() 時,分別計算兩個代數式的值.
時,分別計算兩個代數式的值.
(3)你發現了什么規律?
(4)利用你發現的規律計算:20182-2×2018×2019+20192.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)計算:![]()
(2)計算:(2+![]() )(2﹣
)(2﹣![]() )+
)+![]() ÷
÷![]() +
+![]()
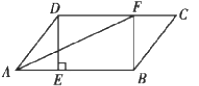
(3)在ABCD中,過點D作DE⊥AB于點E,點F在CD上且DF=BE,連接AF,BF.
①求證:四邊形BFDE是矩形;
②若CF=6,BF=8,AF平分∠DAB,則DF= .
查看答案和解析>>
科目:初中數學 來源: 題型:
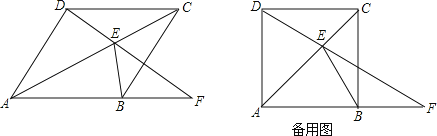
【題目】如圖,四邊形ABCD為菱形,E為對角線AC上的一個動點,連結DE并延長交射線AB于點F,連結BE.
(1)求證:∠AFD=∠EBC;
(2)若∠DAB=90°,當△BEF為等腰三角形時,求∠EFB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y1=k1x+b的圖象與x軸、y軸分別交于A、B兩點,與反比例函數y2=![]() 的圖象分別交于C、D兩點,點D的坐標為(2,-3),點B是線段AD的中點.則不等式 k1x+b —
的圖象分別交于C、D兩點,點D的坐標為(2,-3),點B是線段AD的中點.則不等式 k1x+b —![]() >0的解集是___________.
>0的解集是___________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年四月份,某校在孝感市爭創“全國文明城市” 活動中,組織全體學生參加了“弘揚孝感文化,爭做文明學生”知識競賽,賽后隨機抽取了部分參賽學生的成績,按得分劃分成![]() 六個等級,并繪制成如下兩幅不完整的統計圖表.
六個等級,并繪制成如下兩幅不完整的統計圖表.


請根據圖表提供的信息,解答下列問題:
(1)本次抽樣調查樣本容量為 ,表中:![]() ,
,![]() ;扇形統計圖中,
;扇形統計圖中,![]() 等級對應的圓心角
等級對應的圓心角![]() 等于 度;(4分=1分+1分+1分)
等于 度;(4分=1分+1分+1分)
(2)該校決定從本次抽取的![]() 等級學生(記為甲、乙、丙、丁)中,隨機選擇
等級學生(記為甲、乙、丙、丁)中,隨機選擇![]() 名成為學校文明宣講志愿者,請你用列表法或畫樹狀圖的方法,求恰好抽到甲和乙的概率.
名成為學校文明宣講志愿者,請你用列表法或畫樹狀圖的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列解題過程:已知![]() 、
、![]() 、
、![]() 為△ABC的三邊,且滿足
為△ABC的三邊,且滿足![]() ,
,
試判斷△ABC的形狀.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴△ABC為直角三角形.
問:(1)上述解題過程,從哪一步開始出現錯誤?請寫出該步的代號________;
(2)錯誤的原因是____________________________;
(3)本題的正確結論是_________________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com