
 出相應的t的值和P、Q的坐標;如不可能,請說明理由.
出相應的t的值和P、Q的坐標;如不可能,請說明理由. | 8 |
| 5 |
| 6 |
| 5 |
| 16-t |
| t |
| [(14-t)+(16-2t)]•3 |
| 2 |


科目:初中數學 來源: 題型:
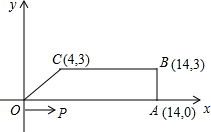 如圖,梯形OABC中,O為直角坐標系的原點,A、B、C的坐標分別為(14,0)、(14,3)、(4,3).點P、Q同時從原點出發,分別作勻速運動,點P沿OA以每秒1個單位向終點A運動,點Q沿OC、CB以每秒2個單位向終點B運動.當這兩點中有一點到達自己的終點時,另一點也停止運動.
如圖,梯形OABC中,O為直角坐標系的原點,A、B、C的坐標分別為(14,0)、(14,3)、(4,3).點P、Q同時從原點出發,分別作勻速運動,點P沿OA以每秒1個單位向終點A運動,點Q沿OC、CB以每秒2個單位向終點B運動.當這兩點中有一點到達自己的終點時,另一點也停止運動.查看答案和解析>>
科目:初中數學 來源: 題型:
| 5 |
 正方形PQRS,設運動時間為t(秒),正方形PQRS與梯形ABCD重疊的面積為S(平方單位).
正方形PQRS,設運動時間為t(秒),正方形PQRS與梯形ABCD重疊的面積為S(平方單位).查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,梯形OABC中,BC∥AO,∠BAO=90°,B(-3
如圖,梯形OABC中,BC∥AO,∠BAO=90°,B(-3| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,梯形OABC中,O為直角坐標系的原點,A、B、C的坐標分別為
如圖,梯形OABC中,O為直角坐標系的原點,A、B、C的坐標分別為查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com