
 AC•BD.
AC•BD.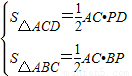
 AC•PD+
AC•PD+ AC•BP
AC•BP AC(PD+PB)=
AC(PD+PB)= AC•B D
AC•B D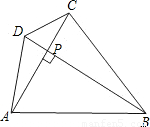
 解:(1)敘述:對角線互相垂直的四邊形的面積等于對角線乘積的一半;
解:(1)敘述:對角線互相垂直的四邊形的面積等于對角線乘積的一半; =
=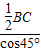 =
= =
= BC=
BC= ,
, ,BD=BP+PD=5
,BD=BP+PD=5 .
. cm
cm •BD•AC=25(cm2)
•BD•AC=25(cm2)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源:同步訓練與評價·數學·八年級·上 題型:044
閱讀材料,解答問題.
①如圖(1)已知正方形ABCD的對角線AC、BD相交于點O,E是AC上一點,過A作AG⊥EB,垂足為G,AG交BD于F,則OE=OF理由是:∵四邊開ABCD是正方形,∴∠BOE=∠AOF=![]() ,BO=AO.又∵AG⊥EB,∠1+∠3=
,BO=AO.又∵AG⊥EB,∠1+∠3=![]() =∠2+∠3∴∠1=∠2,∴Rt△BOE≌Rt△AOF解答此題后某同學產生了如下猜想:對上述命題,若點E在AC的延長線上,AG⊥EB,AG交EB的延長線于G,AG的延長線交DB的延長線于F,其它條件不變,如圖,則仍有OE=OF.問猜想所得的結論是否成立,請說明理由.
=∠2+∠3∴∠1=∠2,∴Rt△BOE≌Rt△AOF解答此題后某同學產生了如下猜想:對上述命題,若點E在AC的延長線上,AG⊥EB,AG交EB的延長線于G,AG的延長線交DB的延長線于F,其它條件不變,如圖,則仍有OE=OF.問猜想所得的結論是否成立,請說明理由.

②已知:E、F分別是平行四邊形ABCD的邊AD和BC的中點,并且2AB=BC,G是AF和BE的交點,H是CE和DF的交點.(1)試探求四邊形GFHE的形狀;并說明理由.(2)若四邊形GFHE是正方形,平行四邊形ABCD應滿足什么條件?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com