
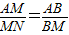 ,根據(jù)(1)的相似三角形可得出
,根據(jù)(1)的相似三角形可得出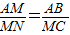 ,因此BM=MC,M是BC的中點.即x=2.
,因此BM=MC,M是BC的中點.即x=2.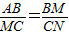 ,即
,即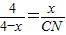 ,
,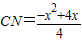 ,
, (
( +4)•4
+4)•4 x2+2x+8
x2+2x+8 (x-2)2+10,
(x-2)2+10,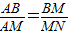 ,
,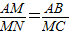 ,
,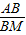 =
=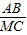 ,
,

 課時訓(xùn)練江蘇人民出版社系列答案
課時訓(xùn)練江蘇人民出版社系列答案 黃岡經(jīng)典趣味課堂系列答案
黃岡經(jīng)典趣味課堂系列答案 啟東小題作業(yè)本系列答案
啟東小題作業(yè)本系列答案科目:初中數(shù)學(xué) 來源: 題型:
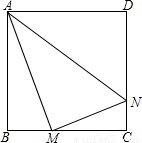
 正方形ABCD邊長為4,M、N分別是BC、CD上的兩個動點,當(dāng)M點在BC上運動時,保持AM和MN垂直.
正方形ABCD邊長為4,M、N分別是BC、CD上的兩個動點,當(dāng)M點在BC上運動時,保持AM和MN垂直.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
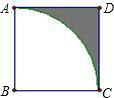 如圖,正方形ABCD邊長為2cm,以點B為圓心,AB的長為半徑作弧
如圖,正方形ABCD邊長為2cm,以點B為圓心,AB的長為半徑作弧 |
| AC |
| A、(4-π)cm2 |
| B、(8-π)cm2 |
| C、(2π-4)cm2 |
| D、(π-2)cm2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 s的速度運動,同時動點Q在線段FC上從F?C以1cm/s的速度運動,動點G在PC上,且∠EGC=∠EQC,連接PD.設(shè)運動時間為t秒.
s的速度運動,同時動點Q在線段FC上從F?C以1cm/s的速度運動,動點G在PC上,且∠EGC=∠EQC,連接PD.設(shè)運動時間為t秒.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
 正方形ABCD邊長為4,M、N分別是BC、CD上的兩個動點,當(dāng)M點在BC上運動時,保持AM和MN垂直,
正方形ABCD邊長為4,M、N分別是BC、CD上的兩個動點,當(dāng)M點在BC上運動時,保持AM和MN垂直,查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com