
寧波濱海水產城一養殖專業戶陳某承包了30畝水塘,分別養殖甲魚和桂魚.有關成本、銷售額見下表:

(1)2011年,陳某養殖甲魚20畝,桂魚10畝.求陳某這一年共收益多少萬元?(收益=銷售額-成本)
(2)2012年,陳某繼續用這30畝水塘全部養殖甲魚和桂魚,計劃投入成本不超過70萬元.若每畝養殖的成本、銷售額與2011年相同,要獲得最大收益,他應養殖甲魚和桂魚各多少畝?
(3)已知甲魚每畝需要飼料500kg,桂魚每畝需要飼料700kg.根據(2)中的養殖畝數,為了節約運輸成本,實際使用的運輸車輛每次裝載飼料的總量是原計劃每次裝載總量的2倍,結果運輸養殖所需全部飼料比原計劃減少了2次.求陳某原定的運輸車輛每次可裝載飼料多少kg?
(1)17萬元;(2)甲魚25畝,桂魚5畝;(3)4000kg
【解析】
試題分析:(1)仔細分析題意及表中數據即可列算式求解;
(2)先設養殖甲魚x畝,則養殖桂魚(30-x)畝列不等式,求出x的取值,再表示出陳某可獲得收益為y萬元函數關系式求最大值;
(3)設陳某原定的運輸車輛每次可裝載飼料a㎏,結合(2)列分式方程求解.
(1)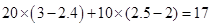 (萬元)
(萬元)
答:陳某這一年共收益17萬元;
(2)設甲魚養殖 畝,則養殖桂魚
畝,則養殖桂魚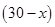 畝,
畝,
由題意知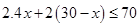
解得
設收益為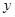 萬元,則
萬元,則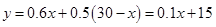
∵函數值y隨x的增大而增大,
∴當 時,
時,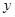 最大值17.5萬元
最大值17.5萬元
答:要獲得最大收益,應養殖甲魚25畝,桂魚5畝;
(3)設陳某原定的運輸車輛每次可裝載飼料a㎏,
由(2)得,共需要飼料為500×25+700×5=16000(㎏),

解得a=4000,
把a=4000代入原方程公分母得,2a=2×4000=8000≠0,
故a=4000是原方程的解.
答:陳某原定的運輸車輛每次可裝載飼料4000㎏.
考點:一次函數的應用,分式方程的應用,一元一次不等式的應用,
點評:解題的關鍵是列不等式求x的取值范圍,再表示出函數關系求最大值,再列分式方程求解.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:2013屆浙江省寧波地區第二學期九年級模擬測試數學試卷(帶解析) 題型:解答題
寧波濱海水產城一養殖專業戶陳某承包了30畝水塘,分別養殖甲魚和桂魚.有關成本、銷售額見下表:
(1)2011年,陳某養殖甲魚20畝,桂魚10畝.求陳某這一年共收益多少萬元?(收益=銷售額-成本)
(2)2012年,陳某繼續用這30畝水塘全部養殖甲魚和桂魚,計劃投入成本不超過70萬元.若每畝養殖的成本、銷售額與2011年相同,要獲得最大收益,他應養殖甲魚和桂魚各多少畝?
(3)已知甲魚每畝需要飼料500kg,桂魚每畝需要飼料700kg.根據(2)中的養殖畝數,為了節約運輸成本,實際使用的運輸車輛每次裝載飼料的總量是原計劃每次裝載總量的2倍,結果運輸養殖所需全部飼料比原計劃減少了2次.求陳某原定的運輸車輛每次可裝載飼料多少kg?
查看答案和解析>>
科目:初中數學 來源:2013年浙江省鄞州八校中考模擬測試數學試卷(解析版) 題型:解答題
寧波濱海水產城一養殖專業戶陳某承包了30畝水塘,分別養殖甲魚和桂魚.有關成本、銷售額見下表:
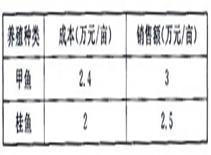
(1) 2011年,陳某養殖甲魚20畝,桂魚10畝.求陳某這一年共收益多少萬元? (收益=銷售額-成本)
(2) 2011年,陳某繼續用這30畝水塘全部養殖甲魚和桂魚,計劃投入成本不超過70萬元.若每畝養殖的成本、銷售額與2011年相同,要獲得最大收益,他應養殖甲魚和桂魚各多少畝?
(3) 已知甲魚每畝需要飼料500kg,桂魚每畝需要飼料700kg.根據(2)中的養殖畝數,為了節約運輸成本,實際使用的運輸車輛每次裝載飼料的總量是原計劃每次裝載總量的2倍,結果運輸養殖所需全部飼料比原計劃減少了2次.求陳某原定的運輸車輛每次可裝載飼料多少kg?
查看答案和解析>>
科目:初中數學 來源: 題型:
寧波濱海水產城一養殖專業戶陳某承包了30畝水塘,分別養殖甲魚和桂魚.有關成本、銷售額見下表:

(1) 2011年,陳某養殖甲魚20畝,桂魚10畝.求陳某這一年共收益多少萬元? (收益=銷售額-成本)
(2) 2012年,陳某繼續用這30畝水塘全部養殖甲魚和桂魚,計劃投入成本不超過70萬元.若每畝養殖的成本、銷售額與2011年相同,要獲得最大收益,他應養殖甲魚和桂魚各多少畝?
(3) 已知甲魚每畝需要飼料500kg,桂魚每畝需要飼料700kg.根據(2)中的養殖畝數,為了節約運輸成本,實際使用的運輸車輛每次裝載飼料的總量是原計劃每次裝載總量的2倍,結果運輸養殖所需全部飼料比原計劃減少了2次.求陳某原定的運輸車輛每次可裝載飼料多少kg?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com