
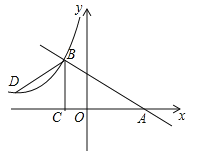
【題目】如圖,長方形ABOD的頂點A是函數y=-x-(k+1)的圖象與函數y=![]() 在第二象限的圖象的交點,B,D兩點在坐標軸上,且長方形ABOD的面積為3.
在第二象限的圖象的交點,B,D兩點在坐標軸上,且長方形ABOD的面積為3.
(1)求兩函數的表達式;
(2)求兩函數圖象的交點A,C的坐標;
(3)若點P是y軸上一動點,且S△APC=5,求點P的坐標.

【答案】(1)反比例函數的表達式為y=-![]() ,一次函數的表達式為y=-x+2(2)點A,C的坐標分別為(-1,3),(3,-1)(3)點P的坐標為(0,
,一次函數的表達式為y=-x+2(2)點A,C的坐標分別為(-1,3),(3,-1)(3)點P的坐標為(0, ![]() )或(0,-
)或(0,-![]() )
)
【解析】試題分析:(1)根據圖象所在的象限結合矩形ABOD的面積,就能求出k的值,進而求出兩函數的表達式;
(2)將兩函數解析式聯立消元,求出其解,即得到交點A、C的坐標;
(3),設點P的坐標為(0,m),直線y=-x+2與y軸的交點坐標為M(0,2),根據S△APC=S△AMP+S△CMP=5解答即可.
試題解析:(1)由圖象知k<0,由已知條件得|k|=3,
∴k=-3.
∴反比例函數的表達式為y=-![]() ,
,
一次函數的表達式為y=-x+2.
(2)由y=-![]() 與y=-x+2可得,-
與y=-x+2可得,- ![]() =-x+2,
=-x+2,
去分母整理后得x2-2x-3=0,
x2-2x+1-4=0,
(x-1)2=4,
∴x-1=±2,
即x1=-1,x2=3.
∴y1=3,y2=-1.
∴點A,C的坐標分別為(-1,3),(3,-1).
(3)設點P的坐標為(0,m),直線y=-x+2與y軸的交點為M,則M的坐標為(0,2).
∵S△APC=S△AMP+S△CMP=![]() ×PM×(|-1|+|3|)=5,
×PM×(|-1|+|3|)=5,
∴PM=![]() ,即|m-2|=
,即|m-2|=![]() .
.
∴m=![]() 或m=-
或m=-![]() .
.
∴點P的坐標為(0, ![]() )或(0,-
)或(0,-![]() ).
).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,函數y= ![]() 的圖象過點A(1,2).
的圖象過點A(1,2). 
(1)求該函數的解析式;
(2)過點A分別向x軸和y軸作垂線,垂足為B和C,求四邊形ABOC的面積;
(3)求證:過此函數圖象上任意一點分別向x軸和y軸作垂線,這兩條垂線與兩坐標軸所圍成矩形的面積為定值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,紙上有五個邊長為1的小正方形組成的圖形紙,我們可以把它剪開拼成一個正方形。

![]()

(1)拼成的正方形的面積與邊長分別是多少?
(2)請在3×3方格圖中,找出連接四個格點組成面積為5的正方形,并在圖中畫出虛線。
(3)你能把十個小正方形組成的圖形紙,剪兩刀并拼成正方形嗎?若能,則它的邊長是多少?并在圖中畫出裁剪的線。


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y=kx+b的圖象與x軸交于點A,與反比例函數![]() (x<0)的圖象交于點B(﹣2,n),過點B作BC⊥x軸于點C,點D(3﹣3n,1)是該反比例函數圖象上一點.
(x<0)的圖象交于點B(﹣2,n),過點B作BC⊥x軸于點C,點D(3﹣3n,1)是該反比例函數圖象上一點.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函數y=kx+b的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2017山東省菏澤市,第20題,7分)如圖,一次函數y=kx+b與反比例函數![]() 的圖象在第一象限交于A、B兩點,B點的坐標為(3,2),連接OA、OB,過B作BD⊥y軸,垂足為D,交OA于C,若OC=CA.
的圖象在第一象限交于A、B兩點,B點的坐標為(3,2),連接OA、OB,過B作BD⊥y軸,垂足為D,交OA于C,若OC=CA.
(1)求一次函數和反比例函數的表達式;
(2)求△AOB的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求解下列方程.
(1)(x﹣3)2=16
(2)x2﹣4x=5(配方法)
(3)x2﹣4x﹣5=0(公式法)
(4)x2﹣5x=0(因式分解法)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按要求解下列方程.
(1)(x﹣3)2=16
(2)x2﹣4x=5(配方法)
(3)x2﹣4x﹣5=0(公式法)
(4)x2﹣5x=0(因式分解法)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c圖象對稱軸是直線x=1,則下列結論:
①a<0,b<0,
②2a﹣b>0,
③a+b+c>0,
④a﹣b+c<0,
⑤當x>1時,y隨x的增大而減小,
其中正確的是( )
A.①②③
B.②③④
C.③④⑤
D.①③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com