
【題目】在平面內正方形ABCD與正方形CEFH如圖放置,連DE,BH,兩線交于M.求證: 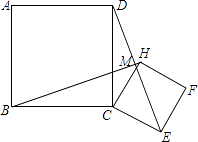
(1)BH=DE.
(2)BH⊥DE.
【答案】
(1)證明:在正方形ABCD與正方形CEFH中,
BC=CD,CE=CH,∠BCD=∠ECH=90°,
∴∠BCD+∠DCH=∠ECH+∠DCH,
即∠BCH=∠DCE,
在△BCH和△DCE中,
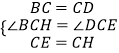 ,
,
∴△BCH≌△DCE(SAS),
∴BH=DE
(2)證明:∵△BCH≌△DCE,
∴∠CBH=∠CDE,
又∵∠CGB=∠MGD,
∴∠DMB=∠BCD=90°,
∴BH⊥DE.
【解析】(1)根據正方形的性質可得BC=CD,CE=CH,∠BCD=∠ECH=90°,然后求出∠BCH=∠DCE,再利用“邊角邊”證明△BCH和△DCE全等,根據全等三角形對應邊相等證明即可;(2)根據全等三角形對應角相等可得∠CBH=∠CDE,然后根據三角形的內角和定理求出∠DMB=∠BCD=90°,再根據垂直的定義證明即可.
【考點精析】通過靈活運用正方形的性質,掌握正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形即可以解答此題.


科目:初中數學 來源: 題型:
【題目】已知點P(2-a,3a+6)到兩坐標軸的距離相等,則點P的坐標為( )
A. (3,3) B. (6,-6) C. (3,3)或(6,-6) D. (3,-3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水資源保護組織對石家莊某小區的居民進行節約水資源的問卷調查.某居民在問卷上的選項代號畫“√”,這個過程是收集數據中的( )
A.確定調查范圍
B.匯總調查數據
C.實施調查
D.明確調查問題
查看答案和解析>>
科目:初中數學 來源: 題型:
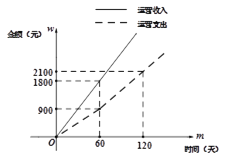
【題目】環保健康的“共享單車”已成為人們短途出行的一種新方式,一輛新投放市場的單車其先期成本為1050元. 如圖是一輛新投放的共享單車其運營收入![]() 和運營支出
和運營支出![]() 關于時間
關于時間![]() 的函數圖象。
的函數圖象。
注:一輛單車的盈利=運營收入-運營支出-先期成本
(1)分別求![]() 及運營60天后
及運營60天后![]() 關于時間
關于時間![]() 的函數關系式.
的函數關系式.
(2)求一輛新投放市場的單車恰好收回先期成本需要運營多少天?
(3)某公司投放市場一批單車,其先期成本不少于2.1萬元但不超過10.5萬元,經過一段時間的市場試運營共盈利3550元,則該公司試運營的天數為 天(直接寫出答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列事件中,是必然事件的是( )
A.購買一張彩票,中獎B.射擊運動員射擊一次,命中靶心
C.任意畫一個三角形,其內角和是180°D.經過有交通信號燈的路口,遇到紅燈
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC的三個頂點的坐標分別為A(-2,3)、B(-6,0)、C(-1,0).
(1)請直接寫出點A關于原點O對稱的點的坐標;
(2)將△ABC繞坐標原點O逆時針旋轉90°,畫出圖形,寫出點B的對應點的坐標;
(3)請直接寫出:以A、B、C為頂點的平行四邊形的第四個頂點D的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com