
【題目】在直角坐標平面內,![]() 為原點,點
為原點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 軸. 點
軸. 點![]() 與點
與點![]() 關于原點對稱,直線
關于原點對稱,直線![]() (
(![]() 為常數)經過點
為常數)經過點![]() ,且與直線
,且與直線![]() 相交于點
相交于點![]() .
.
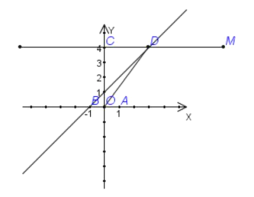
(1)求![]() 的值和點
的值和點![]() 的坐標;
的坐標;
(2)在![]() 軸上有一點
軸上有一點![]() ,使
,使![]() 的面積為
的面積為![]() ,求
,求![]() 點的坐標;
點的坐標;
(3)在![]() 軸的正半軸上是否存在一點
軸的正半軸上是否存在一點![]() ,使得
,使得![]() 為等腰三角形,若存在,求出點
為等腰三角形,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案科目:初中數學 來源: 題型:
【題目】下面的圖象反映的過程是:張強從家跑步去體育場,在那里鍛煉了一陣后又原路返回,順路到文具店去買筆,然后散步回家.其中x表示時間,y表示張強離家的距離.根據圖象回答:
(1)體育場離張強家______ 千米,張強從家到體育場用了______ 分鐘;
(2)體育場離文具店______ 千米;
(3)張強在文具店逗留了______ 分鐘.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AE⊥BC,AF⊥CD,垂足分別為E,F,且BE=DF.
(1)求證:ABCD是菱形;
(2)若AB=5,AC=6,求ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題:如圖(1),點E、F分別在正方形ABCD的邊BC、CD上,∠EAF=45°,試判斷BE、EF、FD之間的數量關系.
(發現證明)小聰把△ABE繞點A逆時針旋轉90°至△ADG,從而發現EF=BE+FD,請你利用圖(1)證明上述結論.
(類比引申)如圖(2),四邊形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,點E、F分別在邊BC、CD上,則當∠EAF與∠BAD滿足 關系時,仍有EF=BE+FD.
(探究應用)如圖(3),在某公園的同一水平面上,四條通道圍成四邊形ABCD.已知AB=AD=80米,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC、CD上分別有景點E、F,∠EAF=75°且AE⊥AD,DF=40(![]() ﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長(結果取整數,參考數據:
﹣1)米,現要在E、F之間修一條筆直道路,求這條道路EF的長(結果取整數,參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
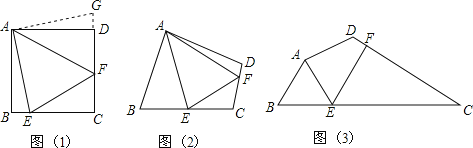
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上,點![]() 表示
表示![]() ,點
,點![]() 表示
表示![]() ,點
,點![]() 表示
表示![]() .動點
.動點![]() 從點
從點![]() 出發,沿數軸正方向以每秒
出發,沿數軸正方向以每秒![]() 個單位的速度勻速運動;同時,動點
個單位的速度勻速運動;同時,動點![]() 從點
從點![]() 出發,沿數軸負方向以每秒
出發,沿數軸負方向以每秒![]() 個單位的速度勻速運動.設運動時間為
個單位的速度勻速運動.設運動時間為![]() 秒.
秒.
(1)當![]() 為何值時,
為何值時,![]() 、
、![]() 兩點相遇?相遇點
兩點相遇?相遇點![]() 所對應的數是多少?
所對應的數是多少?
(2)在點![]() 出發后到達點
出發后到達點![]() 之前,求
之前,求![]() 為何值時,點
為何值時,點![]() 到點
到點![]() 的距離與點
的距離與點![]() 到點
到點![]() 的距離相等;
的距離相等;
(3)在點![]() 向右運動的過程中,
向右運動的過程中,![]() 是
是![]() 的中點,在點
的中點,在點![]() 到達點
到達點![]() 之前,求
之前,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定:將一個平面圖形分成面積相等的兩部分的直線叫做該平面圖形的“等積線”,等積線被 這個平面圖形截得的線段叫做該圖形的“等積線段”(例如三角形的中線就是三角形的等積線段).已 知菱形的邊長為 4,且有一個內角為 60°,設它的等積線段長為 m,則 m 的取值范圍是( )
A. m=4 或 m=4![]() B. 4≤m≤4
B. 4≤m≤4 ![]() C. 2
C. 2 ![]() D. 2
D. 2 ![]() ≤m≤4
≤m≤4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖7,已知平行四邊形ABCD的周長是32cm,AB︰BC=5︰3,AE⊥BC,垂足為E,AF⊥CD,垂足為F,∠EAF=2∠C.
(1)求∠C的度數;
(2)已知DF的長是關于![]() 的方程
的方程![]() -
-![]() -6=0的一個根,求該方程的另一個根.
-6=0的一個根,求該方程的另一個根.
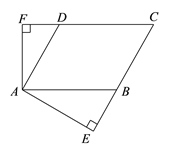
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國古代有著輝煌的數學成就,《周牌算經》、《九章算術》、《海島算經》、《孫子算經》等是我國古代數學的重要文獻.
(1)小聰想從這4部數學名著中隨機選擇1部閱讀,求他選中《九章算術》的概率;
(2)小聰擬從這4部數學名著中選擇2部作為假課外拓展學習內容,用列表或樹狀圖求選中的名著恰好是《九章算術》和《周牌算經》的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com