
| 3 |
| 3 |
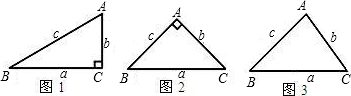 長,不必說明理由.
長,不必說明理由. | 2 |
| 2 |
| 2 |
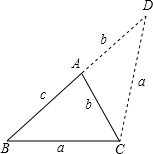
| AD |
| CD |
| CD |
| BD |
| b |
| a |
| a |
| b+c |


科目:初中數學 來源: 題型:閱讀理解
| b |
| 2 |
| b |
| 2 |
 數形結合的思想方法
數形結合的思想方法查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
閱讀下列材料,按要求解答問題:
如圖2-1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通過以下計算:由題意,∠B=30°,∠C=90°,c=2b,a=![]() b,得a2-b2=(
b,得a2-b2=(![]() b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.

于是,小明猜測:對于任意的ΔABC,當∠A=2∠B時,關系式a2-b2=bc都成立.
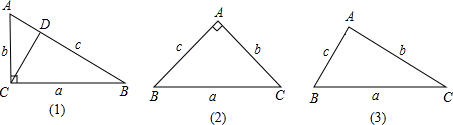
(1)如圖2-2,請你用以上小明的方法,對等腰直角三角形進行驗證,判斷小明的猜測是否正確,并寫出驗證過程;
(2)如圖2-3,你認為小明的猜想是否正確,若認為正確,請你證明;否則,請說明理由;
(3)若一個三角形的三邊長恰為三個連續偶數,且∠A=2∠B,請直接寫出這個三角形三邊的長,不必說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
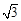 b,得a2-b2=(
b,得a2-b2=(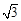 b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.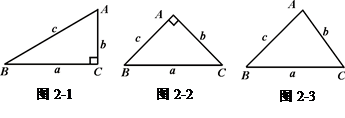
查看答案和解析>>
科目:初中數學 來源:2011-2012學年浙江天門市九年級三輪考試數學卷(一)(解析版) 題型:解答題
閱讀下列材料,按要求解答問題:
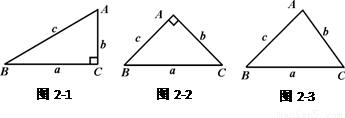
如圖2-1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通過以下計算:由題意,∠B=30°,∠C=90°,c=2b,a=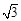 b,得a2-b2=(
b,得a2-b2=(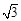 b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.
于是,小明猜測:對于任意的ΔABC,當∠A=2∠B時,關系式a2-b2=bc都成立.
(1)如圖2-2,請你用以上小明的方法,對等腰直角三角形進行驗證,判斷小明的猜測是否正確,并寫出驗證過程;
(2)如圖2-3,你認為小明的猜想是否正確,若認為正確,請你證明;否則,請說明理由;
(3)若一個三角形的三邊長恰為三個連續偶數,且∠A=2∠B,請直接寫出這個三角形三邊的長,不必說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com