
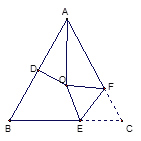
【題目】如圖, ![]() 中,
中, ![]() ,
,![]() ,
, ![]() 的平分線與
的平分線與![]() 的垂直平分線交于點
的垂直平分線交于點![]() ,將
,將![]() 沿
沿![]() (
(![]() 在
在![]() 上,
上, ![]() 在
在![]() 上)折疊,點
上)折疊,點![]() 與點
與點![]() 恰好重合,則
恰好重合,則![]() 的度數是( )
的度數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】試題分析:如圖,連接OB、OC,
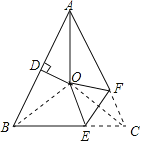
∵∠BAC=54°,AO為∠BAC的平分線,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×54°=27°,
×54°=27°,
又∵AB=AC,
∴∠ABC=![]() (180°-∠BAC)=
(180°-∠BAC)= ![]() (180°-54°)=63°,
(180°-54°)=63°,
∵DO是AB的垂直平分線,
∴OA=OB,
∴∠ABO=∠BAO=27°,
∴∠OBC=∠ABC-∠ABO=63°-27°=36°,
∵AO為∠BAC的平分線,AB=AC,
∴OB=OC,
∴點O在BC的垂直平分線上,
又∵DO是AB的垂直平分線,
∴點O是△ABC的外心,
∴∠OCB=∠OBC=36°,
∵將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,
∴OE=CE,
∴∠COE=∠OCB=36°,
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-36°-36°=108°,
故選:B.


 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,其對稱軸為直線x=﹣1,給出下列結論:(1)b2>4ac; (2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.其中正確的結論有( )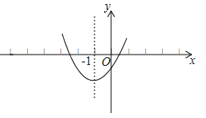
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:AB是⊙O的直徑,DA、DC分別是⊙O的切線,點A、C是切點,連接DO交弧AC于點E,連接AE、CE.
(1)如圖1,求證:EA=EC;
(2)如圖2,延長DO交⊙O于點F,連接CF、BE交于點G,求證:∠CGE=2∠F;
(3)如圖3,在(2)的條件下,DE=![]() AD,EF=2
AD,EF=2![]() , 求線段CG的長.
, 求線段CG的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A在反比例函數y=![]() (x<0)的圖象上,AD∥x軸,AB∥y軸,點B在反比例函數y=
(x<0)的圖象上,AD∥x軸,AB∥y軸,點B在反比例函數y=![]() (x<0)的圖象上,過點B作BC∥x軸,交y軸于點C,若四邊形ABCD的面積為8,則k的值為
(x<0)的圖象上,過點B作BC∥x軸,交y軸于點C,若四邊形ABCD的面積為8,則k的值為 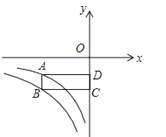
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題:
為了響應“十三五”規劃中提出的綠色環保的倡議,某校文印室提出了每個人都踐行“雙面打印,節約用紙”.已知打印一份資料,如果用A4厚型紙單面打印,總質量為400克,將其全部改成雙面打印,用紙將減少一半;如果用A4薄型紙雙面打印,這份資料的總質量為160克,已知每頁薄型紙比厚型紙輕0.8克,求A4薄型紙每頁的質量.(墨的質量忽略不計)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道|x|的幾何意義是在數軸上數x對應的點與原點的距離,即|x|=|x﹣0|,也就是說|x|表示在數軸上數x與數0對應點之間的距離;這個結論可以推廣為:|x﹣y|表示在數軸上數x、y對應點之間的距離;在解題中,我們常常運用絕對值的幾何意義.
①解方程|x|=2,容易看出,在數軸上與原點距離為2的點對應的數為±2,即該方程的解為x=±2.
②在方程|x﹣1|=2中,x的值就是數軸上到1的距離為2的點對應的數,顯然x=3或x=﹣1.
③在方程|x﹣1|+|x+2|=5中,顯然該方程表示數軸上與1和﹣2的距離之和為5 的點對應的x值,在數軸上1和﹣2的距離為3,滿足方程的x的對應點在1的右邊或﹣2的左邊.若x的對應點在1的右邊,由圖示可知,x=2;同理,若x的對應點在﹣2的左邊,可得x=﹣3,所以原方程的解是x=2或x=﹣3.根據上面的閱讀材料,解答下列問題:
(1)方程|x|=5的解是_______________.
(2)方程|x﹣2|=3的解是_________________.
(3)畫出圖示,解方程|x﹣3|+|x+2|=9.

查看答案和解析>>
科目:初中數學 來源: 題型:
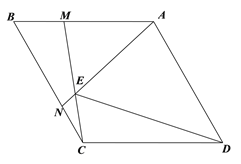
【題目】如圖菱形ABCD中,∠ADC=60°,M、N分別為線段AB,BC上兩點,且BM=CN,且AN,CM所在直線相交于E.
(1)證明△BCM≌△CAN;
(2)∠AEM= °;
(3)求證DE平分∠AEC;
(4)試猜想AE,CE,DE之間的數量關系并證明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com