
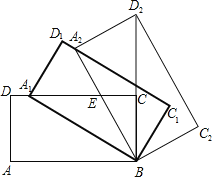
【題目】如圖,矩形ABCD中,AB=m,BC=n,將此矩形繞點B順時針方向旋轉θ(0°<θ<90°)得到矩形A1BC1D1,點A1在邊CD上.
(1)若m=2,n=1,求在旋轉過程中,點D到點D1所經過路徑的長度;
(2)將矩形A1BC1D1繼續繞點B順時針方向旋轉得到矩形A2BC2D2,點D2在BC的延長線上,設邊A2B與CD交于點E,若![]() =
=![]() ﹣1,求
﹣1,求![]() 的值.
的值.
【答案】(1)D到點D1所經過路徑的長度為![]() π;(2)
π;(2)![]() (負根已經舍棄).
(負根已經舍棄).
【解析】(1)作A1H⊥AB于H,連接BD,BD1,則四邊形ADA1H是矩形.解直角三角形,求出∠ABA1,得到旋轉角即可解決問題;
(2)由△BCE∽△BA2D2,推出![]() ,可得CE=
,可得CE=![]() ,由
,由![]() -1推出
-1推出![]() ,推出A1C=
,推出A1C=![]()
![]() ,推出BH=A1C=
,推出BH=A1C=![]()
![]() ,可得m2-n2=6
,可得m2-n2=6![]() ,可得1-
,可得1-![]() =6
=6![]() ,由此解方程即可解決問題;
,由此解方程即可解決問題;
(1)作A1H⊥AB于H,連接BD,BD1,則四邊形ADA1H是矩形.
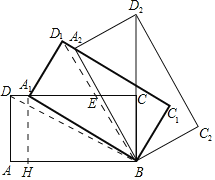
∴AD=HA1=n=1,
在Rt△A1HB中,∵BA1=BA=m=2,
∴BA1=2HA1,
∴∠ABA1=30°,
∴旋轉角為30°,
∵BD=![]() ,
,
∴D到點D1所經過路徑的長度=![]()
(2)∵△BCE∽△BA2D2,
∴![]() ,
,
∴CE=![]()
∵![]() -1
-1
∴![]() ,
,
∴A1C=![]()
![]() ,
,
∴BH=A1C=![]()
![]() ,
,
∴m2-n2=6![]() ,
,
∴m4-m2n2=6n4,
1-![]() =6
=6![]() ,
,
∴![]() (負根已經舍棄).
(負根已經舍棄).


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:
【題目】閱讀下列材料,然后解答后面的問題.
我們知道方程2x+3y=12有無數組解,但在實際生活中我們往往只需要求出其正整數解.例:由2x+3y=12,得![]() ,(x、y為正整數)∴
,(x、y為正整數)∴![]() 則有0<x<6.又
則有0<x<6.又![]() 為正整數,則
為正整數,則![]() 為正整數.
為正整數.
由2與3互質,可知:x為3的倍數,從而x=3,代入![]() .
.
∴2x+3y=12的正整數解為![]()
問題:
(1)請你寫出方程2x+y=5的一組正整數解:______;
(2)若![]() 為自然數,則滿足條件的x值有______個;
為自然數,則滿足條件的x值有______個;
A、2B、3C、4D、5
(3)七年級某班為了獎勵學習進步的學生,購買了單價為3元的筆記本與單價為5元的鋼筆兩種獎品,共花費35元,問有幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
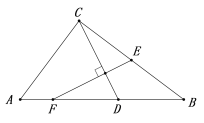
【題目】如圖:在△ABC中,∠ACB =90°,點D在邊AB上,AD=AC,點E在BC邊上,CE=BD,過點E作EF⊥CD交AB于點F,若AF=2,BC=8,則DF的長為_______
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于每個正整數![]() ,設
,設![]() 表示
表示![]() 的末位數字.例如:
的末位數字.例如:![]() (
(![]() 的末位數字),
的末位數字),![]() (
(![]() 的末位數字),
的末位數字),![]() (
(![]() 的末位數字),…則
的末位數字),…則![]() 的值為( )
的值為( )
A.4040B.4038C.0D.4042
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD內部有若干個點,用這些點以及正方形ABCD的頂點A、B、C、D把原正方形分割成一些三角形(互相不重疊):
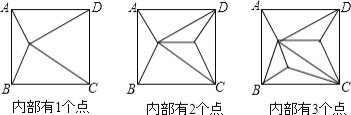
(1)填寫下表:
正方形ABCD內點的個數 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的個數 | 4 | 6 |
|
| … |
|
(2)原正方形能否被分割成2019個三角形?若能,求此時正方形ABCD內部有多少個點?若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上![]() 點表示數
點表示數![]() ,
,![]() 點表示數
點表示數![]() ,
,![]() 點表示數
點表示數![]() ,且
,且![]() 滿足
滿足![]() .
.
(1)![]() ,
,![]() ,
,![]() .
.
(2)若將數軸折疊,使得![]() 點與
點與![]() 點重合,則點
點重合,則點![]() 與表示 的數的點重合;
與表示 的數的點重合;
(3)點![]() 以每秒3個單位長度的速度從點
以每秒3個單位長度的速度從點![]() 向右運動.點
向右運動.點![]() 以每秒2個單位長度的速度從點
以每秒2個單位長度的速度從點![]() 向右運動(點
向右運動(點![]() 、點
、點![]() 同時出發),經過幾秒,點
同時出發),經過幾秒,點![]() 、點
、點![]() 分別到點
分別到點![]() 的距離相等?
的距離相等?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著信息技術的迅猛發展,人們去商場購物的支付方式更加多樣、便捷.某校數學興趣小組設計了一份調查問卷,要求每人選且只選一種你最喜歡的支付方式.現將調查結果進行統計并繪制成如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
(1)這次活動共調查了 人;在扇形統計圖中,表示“支付寶”支付的扇形圓心角的度數為 ;
(2)將條形統計圖補充完整.觀察此圖,支付方式的“眾數”是“ ”;
(3)在一次購物中,小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付,請用畫樹狀圖或列表格的方法,求出兩人恰好選擇同一種支付方式的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC與∠ACB的平分線交于點O,過點O作DE//BC,分別交AB,AC于點D,E,若AB=4,AC=3,則△ADE的周長是_______________。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新定義:對于關于x的一次函數y=kx+b(k≠0),我們稱函數y=![]() 為一次函數y=kx+b(k≠0)的m變函數(其中m為常數).
為一次函數y=kx+b(k≠0)的m變函數(其中m為常數).
例如:對于關于x的一次函數y=x+4的3變函數為y=![]()
(1)關于x的一次函數y=-x+1的2變函數為![]() ,則當x=4時,
,則當x=4時,![]() = ;
= ;
(2)關于x的一次函數y=x+2的1變函數為![]() ,關于x的一次函數y=-
,關于x的一次函數y=-![]() x-2的-1變函數為
x-2的-1變函數為![]() ,求函數
,求函數![]() 和函數
和函數![]() 的交點坐標;
的交點坐標;
(3)關于x的一次函數y=2x+2的1變函數為![]() ,關于x的一次函數y=
,關于x的一次函數y=![]() x-1,的m變函數為
x-1,的m變函數為![]() .
.
①當-3≤x≤3時,函數![]() 的取值范圍是 (直接寫出答案):
的取值范圍是 (直接寫出答案):
②若函數![]() 和函數
和函數![]() 有且僅有兩個交點,則m的取值范圍是 (直接寫出答案).
有且僅有兩個交點,則m的取值范圍是 (直接寫出答案).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com