
【題目】已知代數式A=x2+3xy+x-![]() ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1
(1)當x=y=-2時,求2A-B的值;
(2)若2A-B的值與y的取值無關,求x的值.
【答案】(1)2A-B=7xy+2x-4y;(2)![]()
【解析】
(1)把A與B代入2A﹣B中,去括號合并后,把x與y的值代入計算即可得到結果;
(2)由2A﹣B與x取值無關,確定出y的值即可.
(1)2A﹣B=2(x2+3xy+x﹣![]() )﹣(2x2﹣xy+4y﹣1),
)﹣(2x2﹣xy+4y﹣1),
= 2x2+6xy+2x﹣1﹣2x2+xy﹣4y+1,
=7xy+2x﹣4y,
當x=﹣2,y=﹣2時,2A﹣B=7xy+2x﹣4y =7×(﹣2)×(﹣2)+2×(﹣2)﹣4×(﹣2)=28-4+8=32;
(2)由(1)可知2A﹣B=7xy+2x﹣4y =(7x﹣4)y+2x,
若2A﹣B的值與y的取值無關,則7x﹣4=0,解得:![]() .
.


科目:初中數學 來源: 題型:
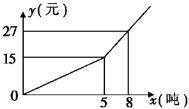
【題目】某市自來水公司為了鼓勵市民節約用水,采取分段收費標準. 若某戶居民每月應繳水費y(元)與用水量x(噸)的函數圖象如圖所示,
(1)分別寫出x≤5和x>5的函數解析式;
(2)觀察函數圖象,利用函數解析式,回答自來水公司采取的收費標準;
(3)若某戶居民六月交水費31元,則用水多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
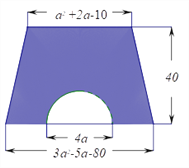
【題目】如圖,梯形的上底為![]() +2
+2![]() -10,下底為3
-10,下底為3![]() -5
-5![]() -80,高為40.(
-80,高為40.(![]() 取3)
取3)
(1)用式子表示圖中陰影部分的面積;
(2)當![]() =10時,求陰影部分面積的值。
=10時,求陰影部分面積的值。
查看答案和解析>>
科目:初中數學 來源: 題型:
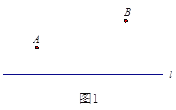
【題目】問題:如圖1,點![]() ,
,![]() 在直線
在直線![]() 的同側,在直線
的同側,在直線![]() 上找一點
上找一點![]() ,使得
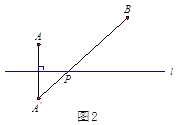
,使得![]() 的值最小.小明的思路是:如圖2,作點
的值最小.小明的思路是:如圖2,作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,連接
,連接![]() ,則
,則![]() 與直線
與直線![]() 的交點
的交點![]() 即為所求.
即為所求.
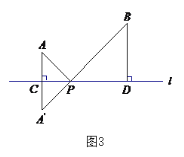
請你參考小明同學的思路,探究并解決下列問題:
(1)如圖3,在圖2的基礎上,設![]() 與直線
與直線![]() 的交點為
的交點為![]() ,過點
,過點![]() 作
作![]() ,垂足為
,垂足為![]() . 若
. 若![]() ,
,![]() ,
,![]() ,寫出
,寫出![]() 的值為____________;
的值為____________;
(2)將(1)中的條件“![]() ”去掉,換成“
”去掉,換成“![]() ”,其它條件不變,寫出此時
”,其它條件不變,寫出此時![]() 的值 ___________;
的值 ___________;
(3)求![]() +
+![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人沿同一路線登山,圖中線段OC、折線OAB分別是甲、乙兩人登山的路程y(米)與登山時間x(分)之間的函數圖象.請根據圖象所提供的信息,解答如下問題:
(1)求甲登山的路程與登山時間之間的函數關系式,并寫出自變量x的取值范圍;
(2)求乙出發后多長時間追上甲?此時乙所走的路程是多少米?
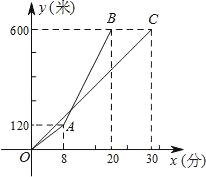
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校實施課程改革,為初三學生設置了A,B,C,D,E,F共六門不同的拓展性課程,現隨機抽取若干學生進行了“我最想選的一門課”調查,并將調查結果繪制成如圖統計圖表(不完整)
選修課 | A | B | C | D | E | F |
人數 | 20 | 30 |
根據圖標提供的信息,下列結論錯誤的是( )

A. 這次被調查的學生人數為200人 B. 扇形統計圖中E部分扇形的圓心角為72°
C. 被調查的學生中最想選F的人數為35人 D. 被調查的學生中最想選D的有55人
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】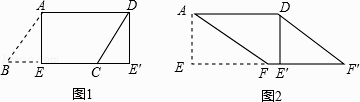
(1)如圖1所示,平行四邊形紙片ABCD中,AD=5,SABCD=15,過點A作AE⊥BC,垂足為E,沿AE剪下△ABE,將它平移至△DCE′的位置,拼成四邊形AEE′D,則四邊形AEE′D是形.
(2)如圖2所示,在(1)中的四邊形紙片AEE′D中,在EE′上取一點F,使EF=4,剪下△AEF,將它平移至△DE′F′的位置,拼成四邊形AFF′D.
①求證:四邊形AFF′D是菱形;
②求四邊形AFF′D兩條對角線的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于點D.
(1)若BC=10,BD=6,則點D到AB的距離是多少?
(2)若∠BAD=30°,求∠B的度數.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com