
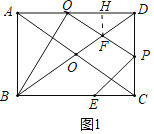
【題目】如圖,在矩形ABCD中,對角線AC,BD相交于點O,AB=3cm,BC=4cm,點E是BC上一點,且CE=1cm.點P由點C出發,沿CD方向向點D勻速運動,速度為1cm/s;點Q由點A出發,沿AD方向向點D勻速運動,速度為![]() cm/s,點P,Q同時出發,PQ交BD于F,連接PE,QB,設運動時間為t(s)(0<t<3).
cm/s,點P,Q同時出發,PQ交BD于F,連接PE,QB,設運動時間為t(s)(0<t<3).
(1)當t為何值時,PE∥BD?
(2)設△FQD的面積為y(cm2),求y與t之間的函數關系式.
(3)是否存在某一時刻t,使得四邊形BQPE的周長最小.若存在,求出此四邊形BQPE的面積;若不存在,請說明理由.

【答案】(1)t=![]() ;(2)
;(2)![]() ;(3)存在,四邊形BQPE的周長的最小值為3+
;(3)存在,四邊形BQPE的周長的最小值為3+![]() .
.
【解析】
(1)當![]() 時,PE∥BD,由此構建方程即可解決問題.
時,PE∥BD,由此構建方程即可解決問題.
(2)作FH⊥DQ.首先證明QF∥OA,△QDF是等腰三角形,求出FH即可解決問題.
(3)如圖2中,作B關于直線AD的對稱點B′,點E關于直線CD的對稱點E′,連接B′E′交AD于Q,交CD于P,連接BQ,PE.此時BQ+QP+PE+BE的值最小.
解:(1)∵四邊形ABCD是矩形,
∴AB=CD=3,AD=BC=4,∠BAD=90°,
![]() ,
,
![]() ,
,
![]() 當
當![]() 時,
時,![]() ,
,
![]()
![]() ,
,
∴t=![]() s時,PE∥BC.
s時,PE∥BC.
(2)如圖1中,作FH⊥DQ.
![]() ,
,![]() ,
,
![]()
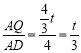 ,
,![]() ,
,
![]()
![]() ,
,
∴FQ∥OA,
∴∠FQD=∠OAD,
∵OA=OD,
∴∠ODA=∠OAD,
∴∠FDQ=∠FQD,
∴FQ=FD,∵FH⊥DQ,
![]() ,
,
![]() ,
,
![]()
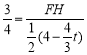 ,
,
![]() ,
,
∴![]() .
.
(3)如圖2中,作B關于直線AD的對稱點B′,點E關于直線CD的對稱點E′,連接B′E′交AD于Q,交CD于P,連接BQ,PE.
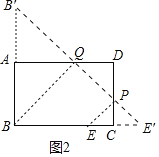
∵BQ+QP+PE+BE=B′Q+QP+PE′+BE=B′E′+BE=B′E′+3,
∴此時BQ+QP+PE+BE的值最小,
![]() ,
,
∴四邊形BQPE的周長的最小值為3+![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=8,AD=17,折疊紙片使點B落在邊AD上的E處,折痕為PQ.當E在AD邊上移動時,折痕的端點P,Q也隨著移動.若限定P,Q分別在邊BA,BC上移動,則點E在邊AD上移動的最大距離為( )
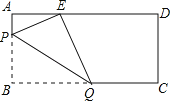
A.6B.7C.8D.9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ACB=90°,AC=BC,點P在邊AB上,點D、Q分別為邊BC上的點,線段AD的延長線與線段PQ的延長線交于點F,連接CP交AF于點E,若∠BPF=∠APC,FD=FQ.
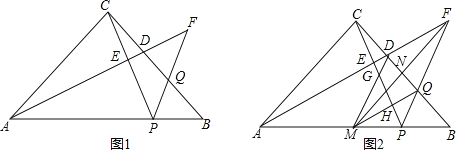
(1)如圖1,求證:AF⊥CP;
(2)如圖2,作∠AFP的平分線FM交AB于點M,交BC于點N,若FN=MN,求證:![]() ;
;
(3)在(2)的條件下,連接DM、MQ,分別交PC于點G、H,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《中學生體質健康標準》規定學生體質健康等級標準:90分及以上為優秀;80分~89分為良好;60分~79分為及格;60分以下為不及格.某校為了解學生的體質健康情況,從八年級學生中隨機抽取了10%的學生進行了體質測試,并將測試數據制成如下統計圖.請根據相關信息解答下面的問題:
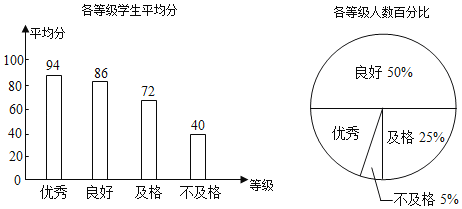
(1)扇形統計圖中,“優秀”等級所在扇形圓心角的度數是多少?
(2)求參加本次測試學生的平均成績;
(3)若參加本次測試“良好”及“良好”以上等級的學生共有35人,請你估計全校八年級“不及格”等級的學生大約有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
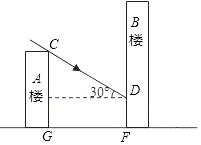
【題目】如圖所示,小明家住在30米高的A樓里,小麗家住在B樓里,B樓坐落在A樓的正北面,已知當地冬至中午12時太陽光線與水平面的夾角為30°.
(1)如果A、B兩樓相距16![]() 米,那么A樓落在B樓上的影子有多長?
米,那么A樓落在B樓上的影子有多長?
(2)如果A樓的影子剛好不落在B樓上,那么兩樓的距離應是多少米?(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
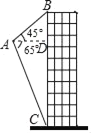
【題目】如圖,航拍無人機從A處測得一幢建筑物頂部B處的仰角為45°、底部C處的俯角為65°,此時航拍無人機A處與該建筑物的水平距離AD為80米.求該建筑物的高度BC(精確到1米).(參考數據:sin65°=0.91,cos65°=0.42,tan65°=2.14)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,經過原點O的拋物線![]() (a≠0)與x軸交于另一點A(
(a≠0)與x軸交于另一點A(![]() ,0),在第一象限內與直線y=x交于點B(2,t).
,0),在第一象限內與直線y=x交于點B(2,t).
(1)求這條拋物線的表達式;
(2)在第四象限內的拋物線上有一點C,滿足以B,O,C為頂點的三角形的面積為2,求點C的坐標;
(3)如圖2,若點M在這條拋物線上,且∠MBO=∠ABO,在(2)的條件下,是否存在點P,使得△POC∽△MOB?若存在,求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將大小相同的正三角形按如圖所示的規律拼圖案,其中第①個圖案中有6個小三角形和1個正六邊形;第②個圖案中有10個小三角形和2個正六邊形;第③個圖案中有14個小三角形和3個正六邊形;…;按此規律排列下去,已知一個小三角形的面積為a,一個正六邊形的面積為b,則第⑧個圖案中所有的小三角形和正六邊形的面積之和為____________.(結果用含a、b的代數式表示)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com