
操作探究:
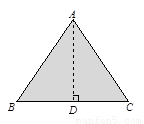
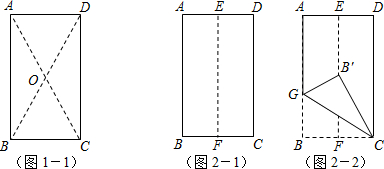
(1)現有一塊等腰三角形紙板,量得周長為32cm,底比一腰多2cm.若把這個三角形紙板沿其對稱軸剪開,拼成一個四邊形,請畫出你能拼成的各種四邊形的示意圖
(2)計算拼成的各個四邊形的兩條對角線長的和.
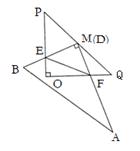
(3)另用紙片制作一個直角邊為4的等腰Rt△OPQ,將(1)中的剪得的Rt△ABD紙片的直角頂點D和PQ的中點M重合(如圖所示),以M為旋轉中心,旋轉Rt△ABD紙片,Rt△ABD紙片的兩直角邊與⊿POQ的兩直角邊分別交于點E、F. 連接EF,探究:在旋轉三角形紙板的過程中,△EOF的周長是否存在最小值,若存在,求出最小值,若不存在。請說明理由。
探究畫圖;19.6;4+2
【解析】
試題分析:(1)

(2) 設AB=AC=xcm,則BC=(x+2)cm,由題意得 解得x=10cm.因此AB=AC=10cm,則BC=12cm,過點A作AD⊥BC于D,∴BD=CD=6cm,∴AD=8cm.
解得x=10cm.因此AB=AC=10cm,則BC=12cm,過點A作AD⊥BC于D,∴BD=CD=6cm,∴AD=8cm.
可以拼成四種四邊形,如上圖所示.
如圖⑴,兩對角線之和為10+10=20cm;
如圖⑵,AD= ,∴兩對角線和為
,∴兩對角線和為 ;
;
如圖⑶,BC= ,∴兩對角線和為
,∴兩對角線和為 ;
;
如圖⑷,∵ ,∴CO=4.8cm,CD=9.6cm.∴兩對角線之和為19.6cm.8分
,∴CO=4.8cm,CD=9.6cm.∴兩對角線之和為19.6cm.8分
(3)答:△EOF的周長存在最小值理由是:連接OM
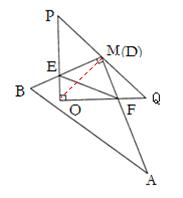
∵ Rt⊿POQ中,OP="OQ" =4,M是PQ的中點
∴OM=PM= PQ=2
PQ=2
∠POM=∠FOM=∠P=45° ∵∠PME+∠EMO=∠OMF+∠EMO
∴∠PME=∠OMF ⊿PME≌⊿OMF
∴ ME=MF
∴ PE=OF ∴OE+OF=OE+PE=OP=4
令OE=x EF=y則y2=x2+(4-x)2=2x2-8x+16
=2(x-2)2+8≥8
當x=2時y2有最小值=8從而 y≥2
故△EOF的周長存在最小值,其最小值是4+2
考點:全等三角形的性質和判定
點評:解答本題的關鍵是熟練掌握判定兩個三角形全等的一般方法:SSS、SAS、ASA、AAS、HL,注意:AAA、SSA不能判定兩個三角形全等,判定兩個三角形全等時,必須有邊的參與,若有兩邊一角對應相等時,角必須是兩邊的夾角.


 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
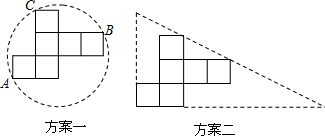
| 紙片被利用的面積 | 紙片的總面積 |
查看答案和解析>>
科目:初中數學 來源: 題型:
| 15 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com