
【題目】已知向量 ![]() 為實數.
為實數.
(1)若 ![]() ,求t的值;
,求t的值;
(2)若t=1,且 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:向量 ![]() 為實數,
為實數,
若 ![]() ,則(2cosα﹣2sinα,sin2α﹣t)=(
,則(2cosα﹣2sinα,sin2α﹣t)=( ![]() ,0),
,0),
可得cosα﹣sinα= ![]() ,平方可得sin2α+cos2α﹣2cosαsinα=
,平方可得sin2α+cos2α﹣2cosαsinα= ![]() ,
,
即為2cosαsinα=1﹣ ![]() =
= ![]() ,(cosα>0,sinα>0),
,(cosα>0,sinα>0),
由sin2α+cos2α=1,解得cosα+sinα= ![]() =
= ![]() =
= ![]() ,
,
即有cosα= ![]() ,sinα=
,sinα= ![]() .
.
則t=sin2α= ![]()
(2)解:若t=1,且 ![]() ,即有4cosαsinα+sin2α=1,
,即有4cosαsinα+sin2α=1,
即有4cosαsinα=1﹣sin2α=cos2α,
由α為銳角,可得cosα∈(0,1),即有tanα= ![]() =
= ![]() ,
,
則tan2α= ![]() =
= ![]() =
= ![]() ,
,
![]() =
= ![]() =
= ![]() =
= ![]()
【解析】(1)運用向量的加減運算和同角的平方關系,即可求得cosα= ![]() ,sinα=
,sinα= ![]() .進而得到t的值;(2)運用向量的數量積的坐標表示,結合條件的商數關系,求得tanα,再由二倍角的正切公式和和角公式,計算即可得到所求值.
.進而得到t的值;(2)運用向量的數量積的坐標表示,結合條件的商數關系,求得tanα,再由二倍角的正切公式和和角公式,計算即可得到所求值.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案科目:初中數學 來源: 題型:
【題目】立定跳遠是小剛同學體育中考的選考項目之一.某次體育課上,體育老師記錄了小剛的一組立定跳遠訓練成績如下表:
成績(m) | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
次數 | 1 | 1 | 2 | 5 | 1 |
則下列關于這組數據的說法中正確的是( )
A.眾數是2.45
B.平均數是2.45
C.中位數是2.5
D.方差是0.48
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=﹣ ![]() x+1的圖象與x軸、y軸分別交于點A、B,以線段AB為邊在第一象限作等邊△ABC.
x+1的圖象與x軸、y軸分別交于點A、B,以線段AB為邊在第一象限作等邊△ABC.
(1)若點C在反比例函數y= ![]() 的圖象上,求該反比例函數的解析式;
的圖象上,求該反比例函數的解析式;
(2)點P(2 ![]() ,m)在第一象限,過點P作x軸的垂線,垂足為D,當△PAD與△OAB相似時,P點是否在(1)中反比例函數圖象上?如果在,求出P點坐標;如果不在,請加以說明.
,m)在第一象限,過點P作x軸的垂線,垂足為D,當△PAD與△OAB相似時,P點是否在(1)中反比例函數圖象上?如果在,求出P點坐標;如果不在,請加以說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖示,若△ABC內一點P滿足∠PAC=∠PBA=∠PCB,則點P為△ABC的布洛卡點.三角形的布洛卡點(Brocard point)是法國數學家和數學教育家克洛爾(A.L.Crelle 1780﹣1855)于1816年首次發現,但他的發現并未被當時的人們所注意,1875年,布洛卡點被一個數學愛好者法國軍官布洛卡(Brocard 1845﹣1922)重新發現,并用他的名字命名.問題:已知在等腰直角三角形DEF中,∠EDF=90°,若點Q為△DEF的布洛卡點,DQ=1,則EQ+FQ=( ) 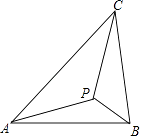
A.5
B.4
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖示AB為⊙O的一條弦,點C為劣弧AB的中點,E為優弧AB上一點,點F在AE的延長線上,且BE=EF,線段CE交弦AB于點D.
①求證:CE∥BF;
②若BD=2,且EA:EB:EC=3:1: ![]() ,求△BCD的面積(注:根據圓的對稱性可知OC⊥AB).
,求△BCD的面積(注:根據圓的對稱性可知OC⊥AB).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知A(﹣4,n),B(2,﹣4)是一次函數y=kx+b的圖象和反比例函數y= ![]() 的圖象的兩個交點.
的圖象的兩個交點. 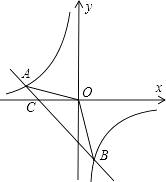
(1)求反比例函數和一次函數的解析式;
(2)求△AOB的面積;
(3)根據圖象直接寫出不等式kx+b< ![]() 時x的解集.
時x的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料: “懷山俊秀,柔水有情”﹣懷柔,一直受到世人的青睞.早在上世紀90年代,聯合國第4屆世界婦女大會NGO論壇的舉辦使懷柔蜚聲海內外,此后,隨著世界養生大會、國際青少年嘉年華、全國汽車拉力賽等一系列活動賽事的成功舉辦,為這座國際交往新城聚集了龐大的人氣.2014年11月11日,全世界的眼光再次聚焦在北京懷柔雁棲湖,這里成功舉辦了第22次APEC領導人峰會.現如今懷柔已成為以自然風光游為基礎,休閑度假游、鄉村美食游、滿族風情游為特色,影視文化游、健身養生游、競技賽事游為時尚的多元化旅游勝地.
隨著懷柔旅游業的迅速發展,也帶動了懷柔的經濟收入.據統計,2011年全年接待游客1047萬人次,比上一年增長5.3%;2012年全年接待游客1085萬人次,比上一年增長3.7%; 2013年全年接待游客1107.6萬人次,比上一年增長2%; 2014年全年接待游客1135萬人次,比上一年增長2.4%;2015年全年接待游客1297.4萬人次,比上一年增長14.3%.(以上數據來源于懷柔信息網)根據以上材料解答下列問題:
(1)用折線圖將2011﹣2015年懷柔區全年接待游客量表示出來,并在圖中標明相應數據;
(2)根據繪制的折線圖中提供的信息,預估 2016年懷柔區全年接待游覽客量約萬人次,你的預估理由是
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com