
【題目】已知,![]() ,點
,點![]() 是直線
是直線![]() 上一個動點(不與
上一個動點(不與![]() 重合),點
重合),點![]() 是
是![]() 邊上一個定點, 過點
邊上一個定點, 過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() ,交直線
,交直線![]() 于點
于點![]() .
.
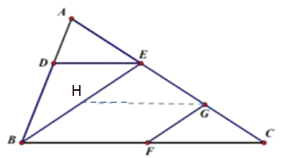
![]() 如圖①,當點
如圖①,當點![]() 在線段
在線段![]() 上時,求證:
上時,求證:![]() .
.

![]() 在
在![]() 的條件下,判斷
的條件下,判斷![]() 這三個角的度數和是否為一個定值? 如果是,求出這個值,如果不是,說明理由.
這三個角的度數和是否為一個定值? 如果是,求出這個值,如果不是,說明理由.
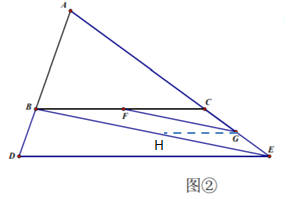
![]() 如圖②,當點
如圖②,當點![]() 在線段
在線段 ![]() 的延長線上時,(2)中的結論是否仍然成立?如果不成立, 請直接寫出
的延長線上時,(2)中的結論是否仍然成立?如果不成立, 請直接寫出![]() 之間的關系.
之間的關系.
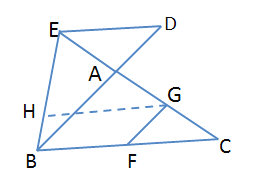
![]() )當點
)當點![]() 在線段
在線段![]() 的延長線上時,(2)中的結論是否仍然成立?如果不成立,請直接 寫出
的延長線上時,(2)中的結論是否仍然成立?如果不成立,請直接 寫出![]() 之間的關系.
之間的關系.

【答案】(1)證明詳見解析;(2)![]() 這三個角的度數和為一個定值,是
這三個角的度數和為一個定值,是![]() ,證明詳見解析;(3)成立;(4)不成立,正確結論為:∠EGF-∠DEC+∠BFG=180°
,證明詳見解析;(3)成立;(4)不成立,正確結論為:∠EGF-∠DEC+∠BFG=180°
【解析】
(1)根據兩條直線平行,內錯角相等,得出![]() ;兩條直線平行,同位角相等,得出
;兩條直線平行,同位角相等,得出![]() ,即可證明
,即可證明![]() .
.
(2)過點![]() 作
作![]() 交BE于點H,根據平行線性質定理,
交BE于點H,根據平行線性質定理,![]() ,
,![]() ,即可得到答案.
,即可得到答案.
(3)過點![]() 作
作![]() 交BE于點H,得到
交BE于點H,得到![]() ,因為
,因為![]() ,所以
,所以![]() ,得到
,得到![]() ,即可求解.
,即可求解.
(4)過點![]() 作
作![]() 交BE于點H,得∠DEC=∠EGH,因為
交BE于點H,得∠DEC=∠EGH,因為![]() ,所以
,所以![]() ,推得∠HGF+∠BFG=180°,即可求解.
,推得∠HGF+∠BFG=180°,即可求解.
(1)∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
(2)![]() 這三個角的度數和為一個定值,是
這三個角的度數和為一個定值,是![]()
過點![]() 作
作![]() 交BE于點H
交BE于點H
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
即![]()
(3)過點![]() 作
作![]() 交BE于點H
交BE于點H
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
即![]()
故![]() 的關系仍成立
的關系仍成立
(4)過點![]() 作
作![]() 交BE于點H
交BE于點H
∴∠DEC=∠EGH
∵![]()
∴![]()
∴∠HGF+∠BFG=180°
∵∠HGF=∠EGF-∠EGH
∴∠HGF=∠EGF-∠DEC
∴∠EGF-∠DEC+∠BFG=180°
∴(2)中的關系不成立,∠EGF、∠DEC、∠BFG之間關系為:∠EGF-∠DEC+∠BFG=180°
故答案為:不成立,∠EGF-∠DEC+∠BFG=180°


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:
【題目】某一出租車一天下午以鼓樓為出發點在東西方向運營,向東走為正,向西走為負,行車里程(單位:km)依先后次序記錄如下:![]() .
.
(1)將最后一名乘客送到目的地,出租車離鼓樓出發點多遠?在鼓樓的什么方向?
(2)若每千米的價格為2.4元,司機一個下午的營業額是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,以△ABC的一邊為邊畫等腰三角形,使得它的第三個頂點在△ABC的其他邊上,則可以畫出的不同的等腰三角形的個數最多為( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A,B,C三人玩籃球傳球游戲,游戲規則是:第一次傳球由A將球隨機地傳給B,C兩人中的某一人,以后的每一次傳球都是由上次的傳球者隨機地傳給其他兩人中的某一人.
(1)求兩次傳球后,球恰在B手中的概率;
(2)求三次傳球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,CA=CB,CD=CE,∠ACB=∠DCE=α.
(1)求證:BE=AD;

(2)當α=90°時,取AD,BE的中點分別為點P、Q,連接CP,CQ,PQ,如圖②,判斷△CPQ的形狀,并加以證明.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖,其對稱軸為直線x=﹣1,給出下列結果:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)a﹣b+c<0.
則正確的結論是( )
A.(1)(2)(3)(4)
B.(2)(4)(5)
C.(2)(3)(4)
D.(1)(4)(5)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD中,AB=2,以點A為圓心,AB為半徑的圓交邊BC于點E,連接DE、AC、AE.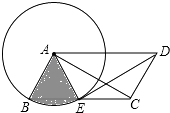
(1)求證:△AED≌△DCA;
(2)若DE平分∠ADC且與⊙A相切于點E,求圖中陰影部分(扇形)的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠A=20°,沿BE將此三角形對折,又沿BA′再一次對折,點C落在BE上的C′處,此時∠C′DB=74°,則原三角形的∠C的度數為( )

A.27°B.59°C.69°D.79°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知A、B在數軸上分別表示a,b.
(1)對照數軸填寫下表:
a | 6 | -6 | -6 | -6 | 2 | -1.5 |
b | 4 | 0 | 4 | -4 | -10 | -1.5 |
A、B兩點的距離 |
(2)若A、B兩點間的距離記為d,試問:d和a,b有何數量關系?
(3)在數軸上找出所有符合條件的整數點P,使它到5和-5的距離之和為10,并求所有這些整數的和;
(4)若點C表示的數為x,當點C在什么位置時,![]() 取得的值最小? 最小值是多少?
取得的值最小? 最小值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com